
 如图,在△ABD中,O为AB的中点,C为DO延长线上一点,∠ACO=135°,∠ODB=45°,探究OD,OC,AC之间相等的数量关系.
如图,在△ABD中,O为AB的中点,C为DO延长线上一点,∠ACO=135°,∠ODB=45°,探究OD,OC,AC之间相等的数量关系. 分析 由条件∠ACO=135°,∠ODB=45°想到角度转移,而O点又是中点,于是想到中线倍长,即延长DO至E,使OE=OD,则△DBO≌△EAO,从而∠AEO=∠BDO=45°,进而得△AEC是等腰直角三角形,于是CE=2AC,而EC=OE-OC=OD-OC,结论显然.
解答 解:延长DO至E,使OE=OD,如图,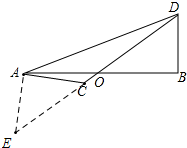
在△DBO和△EAO中,
$\left\{\begin{array}{l}{DO=EO}\\{∠DOB=∠EOA}\\{BO=AO}\end{array}\right.$
∴△DBO≌△EAO(SAS),
∴∠AEO=∠BDO=45°,
∵∠ACO=135°,
∴∠ACE=45°,
∴△AEC是等腰直角三角形,
∴CE=$\sqrt{2}$AC,
∵EC=OE-OC=OD-OC,
∴OD-OC=$\sqrt{2}$AC.
点评 本题主要考查了全等三角形的判定与性质、补角的性质、等腰直角三角形的判定与性质,难度中等.中线倍长是初中几何常用辅助线手段,务必熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$ | B. | $\frac{a}{c}$ | C. | $\frac{b}{c}$ | D. | $\frac{c}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 有一种节能型轿车的油箱最多可装天然气50升,加满燃气后,油箱中的剩余燃气量y(升)与轿车行驶路程x(千米)之间的关系如图所示,根据图象回答下列问题:
有一种节能型轿车的油箱最多可装天然气50升,加满燃气后,油箱中的剩余燃气量y(升)与轿车行驶路程x(千米)之间的关系如图所示,根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
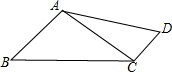 四边形ABCD中,∠B=∠D,∠BAC=120°,∠BCD=150°,若AC=5$\sqrt{3}$,AD=11,则BC的长为7$\sqrt{3}$.
四边形ABCD中,∠B=∠D,∠BAC=120°,∠BCD=150°,若AC=5$\sqrt{3}$,AD=11,则BC的长为7$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com