
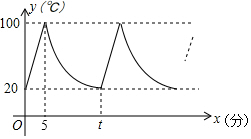
 如图所示,小明家饮水机中原有水的温度是20℃,开机通电后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系.当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系.当水温降至20℃时,饮水机又自动开始加热…,不断重复上述程序.根据图中提供的信息,解答下列问题:
如图所示,小明家饮水机中原有水的温度是20℃,开机通电后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系.当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系.当水温降至20℃时,饮水机又自动开始加热…,不断重复上述程序.根据图中提供的信息,解答下列问题:分析 (1)利用待定系数法代入函数解析式求出即可;
(2)首先求出反比例函数解析式进而得出t的值;
(3)首先求出总时间,再利用每25分钟图象重复出现一次,进而得出答案.
解答 解:(1)当0≤x≤5时,设水温y(℃)与开机时间x(分)的函数关系式为:y=kx+b,
依题意,得$\left\{\begin{array}{l}{b=20}\\{5k+b=100}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=16}\\{b=20}\end{array}\right.$
故所求的函数关系式为:y=16x+20;
(2)在水温下降过程中,设水温y(℃)与开机时间x(分) 的函数关系式为:y=$\frac{m}{x}$,
依题意,得100=$\frac{m}{5}$,
解得:m=500,
故y=$\frac{500}{x}$,
当y=20时,则20=$\frac{500}{t}$,
解得:t=25;
(3)由(2)t=25,结合图象,可知每25分钟图象重复出现一次,
7:20到11:33经历253分钟,
253÷25=10 …3,
∴当x=3时,y=16×3+20=68,
答:饮水机内水温为68℃,共有10次达到100℃.
点评 此题主要考查了一次函数以及反比例函数的应用,根据题意得出正确的函数解析式是解题关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
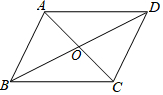 如果平行四边形ABCD的对角线AC、BD相交于O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示向量$\overrightarrow{OC}$.
如果平行四边形ABCD的对角线AC、BD相交于O,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示向量$\overrightarrow{OC}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读材料,回答问题
阅读材料,回答问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com