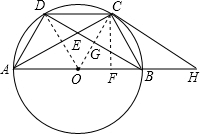
(1)证明:∵C是劣弧

的中点,
∴∠DAC=∠CDB.
∵∠ACD=∠ACD,
∴△DEC∽△ADC.
(2)解:连接OD,
∵
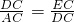
,
∵CE=1,AC=AE+EC=2+1=3,
∴DC
2=AC•EC=3×1=3.
∴DC=

.
∵BC=DC=

,
∵AB是⊙O的直径,
∴∠ACB=90°.
∴AB
2=AC
2+CB
2=3
2+(

)
2=12.
∴AB=

.
∴OD=OB=BC=DC=

.
∴四边形OBCD是菱形.
∴DC∥AB,DC<AB.
∴四边形ABCD是梯形.
法一:
过C作CF垂直AB于F,连接OC,则OB=BC=OC=

,
∴∠OBC=60°.
∴sin60°=
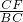
,
CF=BC•sin60°=
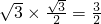
.
∴S
梯形ABCD=

CF(AB+DC)=
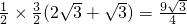
.
法二:(接上证得四边形ABCD是梯形)
∵DC∥AB,
∴AD=BC.
连接OC,则△AOD,△DOC和△OBC的边长均为

的等边三角形.
∴△AOD≌△DOC≌△OBC.
∴S
梯形ABCD=3•S
△AOD=

.
(3)证明:连接OC交BD于G.
由(2)得四边形OBCD是菱形.
∴OC⊥BD且OG=GC.
∵OB=BH,
∴BG∥CH.
∴∠OCH=∠OGB=90°.
∴CH是⊙O的切线.
分析:(1)C是劣弧

的中点,根据等弧所对的圆周角相等就可以证明角相等,从而证明△DEC∽△ADC;
(2)首先利用(1)的结论求出DC,再利用勾股定理计算AB,根据计算结果可以判定四边形OBCD是菱形,然后判断四边形ABCD是梯形;
(3)利用(2)的结论OC⊥BD,OG=GC,再利用平行线的判定方法知道BG∥CH,这样根据切线的判定方法就可以判定了.
点评:此题综合性比较强,把梯形放在圆中,解题利用了梯形的判定和面积公式,解直角三角形,圆的切线的判定等几个知识点.

 的中点,AC交BD于点E,AE=2,EC=1.
的中点,AC交BD于点E,AE=2,EC=1.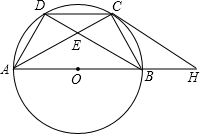 不是,请说明理由.
不是,请说明理由. (1)证明:∵C是劣弧
(1)证明:∵C是劣弧 的中点,
的中点,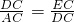 ,
, .
. ,
, )2=12.
)2=12. .
. .
. ,
,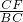 ,
,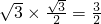 .
. CF(AB+DC)=
CF(AB+DC)=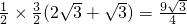 .
. 的等边三角形.
的等边三角形. .
. 的中点,根据等弧所对的圆周角相等就可以证明角相等,从而证明△DEC∽△ADC;
的中点,根据等弧所对的圆周角相等就可以证明角相等,从而证明△DEC∽△ADC;

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°. 如图,点A的坐标为(2
如图,点A的坐标为(2