
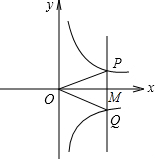
 如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=
如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=| k1 |
| x |
| k2 |
| x |
| PM |
| QM |
| k1 |
| k2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PM |
| QM |
| k1 |
| k2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 (2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=
(2012•临沂)如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数y=| k1 |
| x |
| k2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
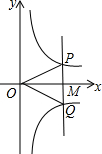 如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=
如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=| k1 |
| x |
| k2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=
如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数y=| k1 |
| x |
| k2 |
| x |
| PM |
| QM |
| k1 |
| k2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州萧山回澜初中九年级12月阶段性测试数学试卷(解析版) 题型:选择题
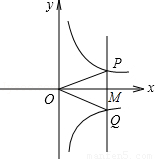
如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数 和
和 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
A.∠POQ不可能等于90°
B.
C.这两个函数的图象一定关于x轴对称
D.△POQ的面积是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com