
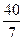 --------------------------------- 1分
--------------------------------- 1分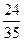 -----------------------------1分
-----------------------------1分

科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗?试说明理由。
向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗?试说明理由。
查看答案和解析>>
科目:初中数学 来源:2011年南京市溧水县中考数学一模试卷 题型:解答题
【改编】(本小题满分6分)
端午节吃粽子是中华民族的传统习俗,五月初五早上,奶奶为小明准备了四只粽子:一
只肉馅,一只香肠馅,两只红枣馅,四只粽子除内部馅料不同外其他均一切相同。小明喜欢
吃红枣馅的粽子。
(1)请你用树状图为小明预测一下吃两只粽子刚好都是红枣馅的概率;
(2)在吃粽子之前,小明准备用一格均匀的正四面体骰子(如图所示)进行吃粽子的模拟试验,规定:掷得点数1向上代表肉馅,点数2向上代表香肠馅,点数3, 向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗?试说明理由。
向上代表红枣馅,连续抛掷这个骰子两次表示随机吃两只粽子,从而估计吃两只粽子刚好都是红枣馅的概率。你认为这样模拟正确吗?试说明理由。
查看答案和解析>>
科目:初中数学 来源:2011年南京市溧水县中考数学一模试卷 题型:解答题
【改编】(本小题满分10分)
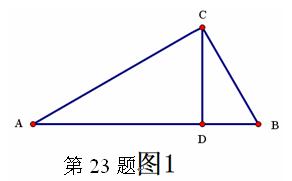
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即“以数解形”;或者借助形的 几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
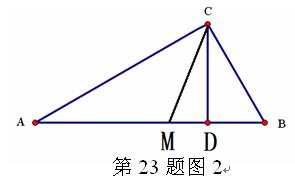
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解:设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com