
 如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | 2 |
分析 连接CE,求出△ABD≌△CBE,根据全等三角形的性质得出AD=CE=4,求出∠CDE=90°,根据勾股定理求出CD即可.
解答 解:连接CE,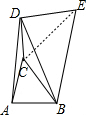
∵∠ABC=∠DBE=50°,
∴∠ABD=∠CBE,
在△ABD和△CBE中
$\left\{\begin{array}{l}{AB=CB}\\{∠ABD=∠CBE}\\{BD=BE}\end{array}\right.$
∴△ABD≌△CBE(SAS),
∴AD=CE=4,
∵BD=BE,∠DBE=50°,
∴∠BDE=∠BED=$\frac{1}{2}$×(180°-∠DBE)=65°,
∵∠BDC=25°,
∴∠CDE=65°+25°=90°,
在Rt△CDE中,由勾股定理得:CD=$\sqrt{C{E}^{2}-D{E}^{2}}$=$\sqrt{{4}^{2}-(\sqrt{13})^{2}}$=$\sqrt{3}$,
故选B.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质,三角形内角和定理,勾股定理的应用,能构造直角三角形是解此题的关键.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:选择题
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
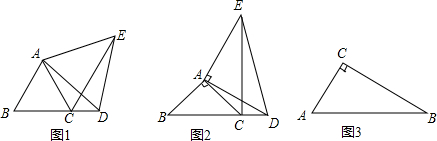
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 全国人口 (亿人) | 儿童人口 (亿人) | 儿科医生 (万人) | 每千名儿童拥有的儿科医生数 |
| 2000 | 12.67 | 2.9 | 9.57 | 0.33 |
| 2005 | 13.06 | 2.65 | 10.07 | 0.38 |
| 2010 | 13.4 | 2.22 | 10.43 | 0.47 |
| 2015 | 13.7 | 2.26 | 9.72 | 0.43 |
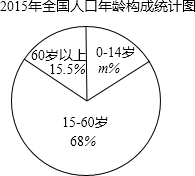
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
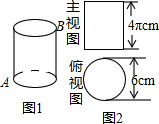 图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )
图中圆柱的主视图与俯视图如图所示,一只蚂蚁从A点沿着圆柱的侧面爬行到B点的最短路线长为( )| A. | (6+4π)cm | B. | 2$\sqrt{9+{π}^{2}}$cm | C. | 7πcm | D. | 5πcm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com