
 如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$.
如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$. 分析 作BG⊥EF、延长EF交BC延长线于点H,设AE=x,则DE=4x、AD=BC=5x,证?AEHC得AE=CH=x、证△DEF∽△CHF得$\frac{DF}{CF}$=$\frac{DE}{CH}$=$\frac{4x}{x}$=4,即DF=4CF,即可设CF=a,则DF=4a,再证△BGC∽△FCH后,设∠ABE=α,可得∠DEF=∠H=2α,由∠EBG=90°-∠ABE-∠HBG=90°-α-(90°-2α)=α=∠ABE结合∠BAE=∠BGE=90°、BE=BE,可证△ABE≌△GBE得AB=BG=5a,由$\frac{BG}{BH}=\frac{FC}{FH}$得FH=$\frac{6x}{5}$,根据勾股定理得FC=$\sqrt{F{H}^{2}-H{C}^{2}}$=$\frac{\sqrt{11}}{5}x$,即a=$\frac{\sqrt{11}}{5}x$,可知AB=5a=$\sqrt{11}$x,在Rt△ABE中由AB2+AE2=BE2得x=1,从而可得DF、DE的长,最后利用勾股定理可得答案.
解答 解:如图,过点B作BG⊥EF于点G,延长EF交BC延长线于点H,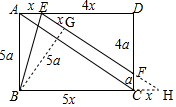
设AE=x,则DE=4x,AD=BC=5x,
∵AB∥CD,EF∥AC,
∴四边形AEHC是平行四边形,
∴AE=CH=x,
∵DE∥CH,
∴△DEF∽△CHF,
∴$\frac{DF}{CF}$=$\frac{DE}{CH}$=$\frac{4x}{x}$=4,即DF=4CF,
设CF=a,则DF=4a,
又∵∠BGH=∠FCH=90°,∠BHG=∠FHC,
∴△BGC∽△FCH,
设∠ABE=α,则∠DEF=∠H=2α,
∴∠HBG=90°-∠H=90°-2α,
∴∠EBG=90°-∠ABE-∠HBG=90°-α-(90°-2α)=α=∠ABE,
∵∠BAE=∠BGE=90°,BE=BE,
∴△ABE≌△GBE,
∴AB=BG=5a,
∵$\frac{BG}{BH}=\frac{FC}{FH}$,即$\frac{5a}{6x}=\frac{a}{FH}$,
∴FH=$\frac{6x}{5}$,
则FC=$\sqrt{F{H}^{2}-H{C}^{2}}$=$\sqrt{(\frac{6x}{5})^{2}-{x}^{2}}$=$\frac{\sqrt{11}}{5}x$,即a=$\frac{\sqrt{11}}{5}x$
∴AB=5a=$\sqrt{11}$x,
在Rt△ABE中,由AB2+AE2=BE2得11x2+x2=(2$\sqrt{3}$)2,
解得:x=1或x=-1(舍),
则DF=4a=$\frac{4\sqrt{11}}{5}$x=$\frac{4\sqrt{11}}{5}$,DE=4,
∴EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\frac{24}{5}$,
故答案为:$\frac{24}{5}$.
点评 本题主要考查相似三角形的判定与性质、矩形的性质、平行四边形的判定与性质、全等三角形的判定与性质及勾股定理等知识点,根据题中线段的比值及角度的关系转化为相似问题和全等问题求解是解题的切入点.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
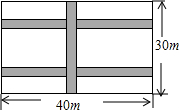 张明的父亲打算在院子里种上蔬菜.已知院子是东西长为40m,南北宽为30m的长方形,为了行走方便,要修筑同样宽的三条道路(如图),东西方向两条,南北方向一条.南北方道路垂直于东西道路,余下的部分分别种上蔬菜.若每条道路的宽为1m,求种蔬菜的土地的总面积.
张明的父亲打算在院子里种上蔬菜.已知院子是东西长为40m,南北宽为30m的长方形,为了行走方便,要修筑同样宽的三条道路(如图),东西方向两条,南北方向一条.南北方道路垂直于东西道路,余下的部分分别种上蔬菜.若每条道路的宽为1m,求种蔬菜的土地的总面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
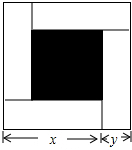 如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个长方形的两边长(x>y),观察图案,指出以下关系式:①x-y=n;②xy=$\frac{{m}^{2}-{n}^{2}}{4}$;③x2-y2=mn;④x2+y2=$\frac{{m}^{2}-{n}^{2}}{2}$.其中正确的关系式的有①②③.
如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个长方形的两边长(x>y),观察图案,指出以下关系式:①x-y=n;②xy=$\frac{{m}^{2}-{n}^{2}}{4}$;③x2-y2=mn;④x2+y2=$\frac{{m}^{2}-{n}^{2}}{2}$.其中正确的关系式的有①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
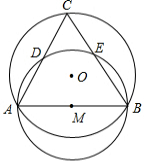 如图,⊙O的半径为2,弦AB的长为2$\sqrt{3}$,以AB为直径作⊙M,点C是优弧$\widehat{AB}$上的一个动点,连接AC、BC,分别交⊙M于点D、E,则线段CD的最大值为2.
如图,⊙O的半径为2,弦AB的长为2$\sqrt{3}$,以AB为直径作⊙M,点C是优弧$\widehat{AB}$上的一个动点,连接AC、BC,分别交⊙M于点D、E,则线段CD的最大值为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com