
 如图,直线y=-x-1交两坐标轴于A、B两点,⊙M经过A、B两点,交x轴正半轴于点C,延长BM交⊙M于D,反比例函数
如图,直线y=-x-1交两坐标轴于A、B两点,⊙M经过A、B两点,交x轴正半轴于点C,延长BM交⊙M于D,反比例函数 >0)的图象经过点D,若C(2,0),则k=________.
>0)的图象经过点D,若C(2,0),则k=________. OA=
OA= ,利用勾股定理可计算出BC=
,利用勾股定理可计算出BC= ,根据圆周角定理得到∠DAB=90°,∠ADB=∠OCB,易证得Rt△ADB∽Rt△OCB,则BD:BC=AB:OB,即BD:
,根据圆周角定理得到∠DAB=90°,∠ADB=∠OCB,易证得Rt△ADB∽Rt△OCB,则BD:BC=AB:OB,即BD: =
= :1,可得到BD=
:1,可得到BD= ,在Rt△ADB中,运用勾股定理计算AD=2
,在Rt△ADB中,运用勾股定理计算AD=2 ,由于∠OAB=45°,∠DAB=90°得到∠DAE=90°-45°=45°,于是得到△ADE为等腰直角三角形,AE=DE=
,由于∠OAB=45°,∠DAB=90°得到∠DAE=90°-45°=45°,于是得到△ADE为等腰直角三角形,AE=DE= ×2
×2 =2,则OE=1,可确定D点坐标,然后利用待定系数法克确定k的值.
=2,则OE=1,可确定D点坐标,然后利用待定系数法克确定k的值.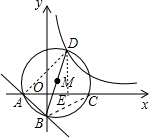
 OA=
OA= ,
, =
= ,
, AD,
AD, =
= :1,
:1, ,
,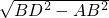 =
= =2
=2 ,
, ×2
×2 =2,
=2, 得k=1×2=2.
得k=1×2=2.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=| 4 |
| x |
| A、8 | ||
| B、6 | ||
| C、4 | ||
D、6
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com