
【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.
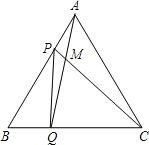
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)请求出何时△PBQ是直角三角形?
【答案】(1)不变,∠CMQ=60°;(2)当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.
【解析】
试题分析:(1)先根据全等三角形的判定定理得出△ABQ≌△CAP,由全等三角形的性质可知∠BAQ=∠ACP,故∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°,故可得出结论;
(2)设时间为t秒,则AP=BQ=tcm,PB=(4﹣t)cm,当∠PQB=90°时,因为∠B=60°,所以PB=2BQ,即4﹣t=2t故可得出t的值,当∠BPQ=90°时,同理可得BQ=2BP,即t=2(4﹣t),由此两种情况即可得出结论.
解:(1)不变,∠CMQ=60°.
∵△ABC是等边三角形,
∴等边三角形中,AB=AC,∠B=∠CAP=60°
又∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.
∴AP=BQ,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°;
(2)设时间为t秒,则AP=BQ=tcm,PB=(4﹣t)cm,
当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,即4﹣t=2t,t=![]() ,
,
当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(4﹣t),t=![]() ,
,
∴当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】有下列命题:①无理数就是开方开不尽的数;②一个实数的立方根不是正数就是负数;③无理数包括正无理数,0,负无理数;④如果一个数的立方根是这个数本身,那么这个数是1或0.其中假命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.

(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°,AC=4.
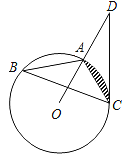
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某班的一次语文测验中,有6名同学不及格,不及格率为12.5%,同时也有9名同学优秀,则这个班在这次测验中的优秀率为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
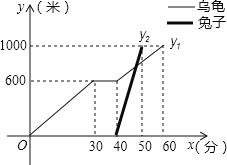
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,正确的是( )
A. t5·t5 = 2t5 B. t4+t2 = t 6 C. t3·t4 = t12 D. t2·t3 = t5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com