
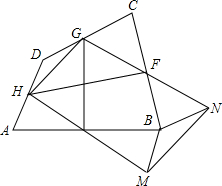
 如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号________;请利用三条裁剪线将原图形剪拼成一个与之面积相等的平行四边形,在图中画出裁剪线及剪拼成的平行四边形.
如图,一任意四边形纸片ABCD中,E,F,G,H为各边中点,则EG与HF的关系为:①相等;②互相垂直;③互相平分;④垂直平分;⑤相等且垂直.请选择正确序号________;请利用三条裁剪线将原图形剪拼成一个与之面积相等的平行四边形,在图中画出裁剪线及剪拼成的平行四边形. EF,再利用平行四边形的判定与性质得出EG与HF的关系,再利用图形的平移与中心对称得出裁剪方法即可.
EF,再利用平行四边形的判定与性质得出EG与HF的关系,再利用图形的平移与中心对称得出裁剪方法即可. 解;如图1所示:连接AC,
解;如图1所示:连接AC, AC,EF∥AC,EF=
AC,EF∥AC,EF= AC,
AC, EF,
EF, 故答案为:③;
故答案为:③;

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
 20、现将三张形状、大小完全相同的平行四边形透明纸片,分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形纸片的每个顶点与小正方形的顶点重合(如图1、图2、图3).
20、现将三张形状、大小完全相同的平行四边形透明纸片,分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形纸片的每个顶点与小正方形的顶点重合(如图1、图2、图3).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011--2012学年北京西城实验学校初二期中数学试卷(解析版) 题型:解答题
如图8-1、9-1,现将二张形状、大小完全相同的平行四边形透明纸片,分别放在方格纸中,方格纸中的每个小正方形的边长均为1,并且平行四边形纸片的每个顶点与小正方形的顶点重合.分别在图8-1、图9-1中,经过平行四边形纸片的任意一个顶点画一条裁剪线,沿此裁剪线将平行四边形纸片裁成两部分,按所采裁图形的实际大小,在图8-2中拼成正方形,在图9-2中拼成一个角是135° 的三角形.
要求:
(1)裁成的两部分在拼成几何图形时要互不重叠且不留空隙;
(2)所拼出的几何图形的各顶点必须与小正方形的顶点重合.

查看答案和解析>>
科目:初中数学 来源:2008年江苏省泰州市兴化市板桥一中中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《尺规作图》(01)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com