

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
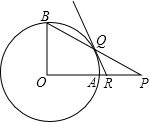 (1998•安徽)已知⊙O中OA、OB是两条互相垂直的半径,P为OA延长线上任一点,BP与⊙O相交于Q,过Q作⊙O的切线QR与OP相交于R.
(1998•安徽)已知⊙O中OA、OB是两条互相垂直的半径,P为OA延长线上任一点,BP与⊙O相交于Q,过Q作⊙O的切线QR与OP相交于R.查看答案和解析>>
科目:初中数学 来源: 题型:
 |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省无锡市惠山区九年级下学期期中考试数学卷 题型:解答题
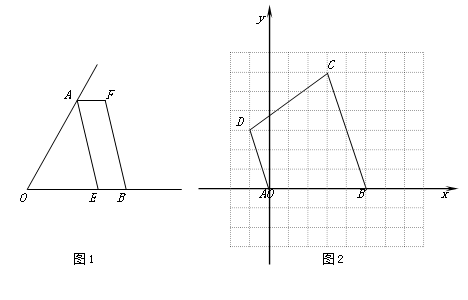
(本题10分)(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF 是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线.(保留作图痕迹,不要求写作法)
(2)如图2,在10×10的正方形网格中,点A(0,0)、B(5,0)、C(3,6)、D(-1,3),
①依次连结A、B、C、D四点得到四边形ABCD,四边形ABCD的形状是 ▲ .
②在x轴上找一点P,使得△PCD的周长最短(直接画出图形,不要求写作法);
此时,点P的坐标为 ▲ ,最短周长为 ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com