
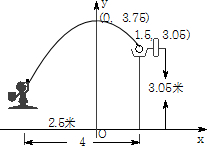
 在一场篮比赛中,甲球员在距篮4米处跳投,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.75米,然后球准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
在一场篮比赛中,甲球员在距篮4米处跳投,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.75米,然后球准确落入篮圈.已知篮圈中心到地面的距离为3.05米.| 14 |
| 45 |
| 14 |
| 45 |
| 14 |
| 45 |
| 14 |
| 45 |


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
 如图所示,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点时网格线的交点)和点A1.
如图所示,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点时网格线的交点)和点A1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com