练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

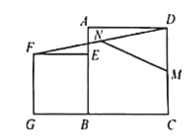
    【题目】如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN.若AB=7，BE=5，则MN=_______.

    【答案】

    【解析】

    连接FC，根据三角形中位线定理可得FC=2MN，继而根据四边形ABCD，四边形EFGB是正方形，推导得出G、B、C三点共线，然后再根据勾股定理可求得FC的长，继而可求得答案.

    连接FC，∵M、N分别是DC、DF的中点，

    ∴FC=2MN，

    ∵四边形ABCD，四边形EFGB是正方形，

    ∴∠FGB=90°，∠ABG=∠ABC=90°，FG=BE=5，BC=AB=7，

    ∴∠GBC=∠ABG+∠ABC=180°，

    即G、B、C三点共线，

    ∴GC=GB+BC=5+7=12，

    ∴FC==13，

    ∴MN=，

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

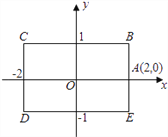
    【题目】如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2012次相遇地点的坐标是（ ）

    A. （2，0） B. （﹣1，1） C. （﹣2，1） D. （﹣1，﹣1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

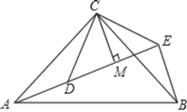
    【题目】如图，△ACB和△DCE均为等腰三角形，∠ACB＝∠DCE＝90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．

    （1）求∠AEB的度数；

    （2）线段CM、AE、BE之间存在怎样的数量关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小区改善生态环境，实行生活垃圾的分类处理，将生活垃圾分成三类：厨房垃圾、可回收垃圾和其他垃圾，分别记为m，n，p，并且设置了相应的垃圾箱，“厨房垃圾”箱，“可回收垃圾”箱和“其他垃圾”箱，分别记为A，B，C.

    (1)若将三类垃圾随机投入三类垃圾箱，请用画树状图的方法求垃圾投放正确的概率；

    (2)为了了解居民生活垃圾分类投放的情况，现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾，数据统计如下(单位：吨)：

    A

    B

    C

    m

    400

    100

    100

    n

    30

    240

    30

    p

    20

    20

    60

    请根据以上信息，试估计“厨房垃圾”投放正确的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（　　）

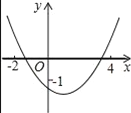
    A. c＞﹣1 B. b＞0 C. 2a+b≠0 D. 9a+c＞3b

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD，尺规作图：以点A为圆心，AB的长为半径画弧交AD于点F，分别以点B，F为圆心，以大于 BF的长为半径画弧交于点G，做射线AG交BC与点E，若BF=12，AB=10，则AE的长为（ ）．

    A.17B.16C.15D.14

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本小题满分8分）某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个，且制成一个甲盒比制作一个乙盒需要多用20%的材料。

    （1）求制作每个甲盒、乙盒各用多少材料？

    （2）如果制作甲、乙两种包装盒3000个，且甲盒的数量不少于乙盒数量的2倍，那么请写出所需材料总长度与甲盒数量之间的函数关系式，并求出最少需要多少米材料。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，，作斜边AB上中线CD，得到第1个三角形ACD；于点E，作斜边DB上中线EF，得到第2个三角形DEF；依次作下去则第1个三角形的面积等于______，第n个三角形的面积等于______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC于点E，交AB的延长线于点F．

    （1）判断直线DE与⊙O的位置关系，并说明理由；

    （2）如果AB=5，BC=6，求DE的长．

    查看答案和解析>>

    同步练习册答案