
菱形具有而一般平行四边形不具有的性质是( )
A、对角相等 B、对角线互相垂直
C、对边平行 D、对边相等
B
【解析】
试题分析:菱形具有平行四边形的全部性质,比较菱形和平行四边形的性质即可解题.
平行四边形的对角相等,对角线互相平分,对边平行且相等,故A、C、D选项错误,
对角线互相垂直的平行四边形为菱形,故B选项正确,
故选 B.
考点:1.菱形的性质;2.平行四边形的性质.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:判断题
(本题12分)如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.

(1)求a,b的值;(3分)
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM∥OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(4分)
(3)如图(3),将直线AB绕点A顺时针旋转15度交抛物线对称轴于点C, 点P为线段OA上的一个动点(与点O、点A不重合),以点O为圆心、以OP为半径的圆弧与线段OC交于点M,以点A为圆心、以AP为半径的圆弧与线段AC交于点N,连接MN.在点P运动的过程中,四边形OMNA的面积有最大值还是有最小值?请求出该值.(5分)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市七年级下学期第一次月考数学试卷(解析版) 题型:选择题
PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )
A、0.25×10-5 B、0.25×10-6
C、2.5×10-5 D、2.5×10-6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:填空题
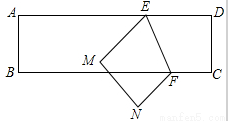
如图,把一个长方形的纸片沿EF折叠后, 点D、C分别落在点M、N的位置, 如果∠EFB=65,那么∠AEM等于 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,边长为1的正方形ABCD绕点A逆时针旋转30得到正方形AEFG,则它们的公共部分面积等于( )

A、 B、1-
B、1- C、1-
C、1- D、
D、
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市高港实验学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题10分)如图,正方形网格中每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点的三角形叫做格点三角形.

(1)格点△ABC的面积为 ;
(2)画出格点△ABC绕点C逆时针旋转90°后的△A1B1C1,并求出在旋转过程中,点B所经过的路径长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省泰州市高港实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
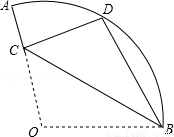
如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在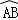 上的点D处,折痕交OA于点C,则
上的点D处,折痕交OA于点C,则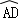 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省七年级上学期第一次质检数学试卷(解析版) 题型:解答题
一只小狗从某地出发在一直线上来回跑,假定向右跑记为为正数,向左跑记为负数,记录小狗跑动的各段路程依次为(单位:米):+5,-3,+10,-8,-6,+12,-10.求:
(1)小狗最后是否回到出发点?
(2)在跑动过程中,如果每跑动1米奖励小狗2粒狗粮,则小狗一共得到多少粒狗粮?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区七年级上学期期中考试数学试卷(解析版) 题型:选择题
已知(a+3)2+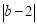 =0,则ab的值是( )
=0,则ab的值是( )
A.-6 B.6 C.-9 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com