
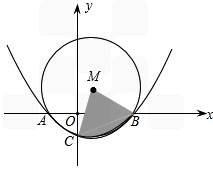
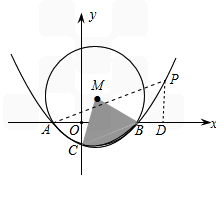
| 解:(1)∵点(﹣1,0)、(m,0)在抛物线y=ax2+bx﹣1上 ∴  , ,解得 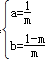 ∴抛物线对应的函数表达式为: 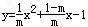 ; ;(2)在抛物线对应的函数表达式中,令x=0,得y=﹣1, ∴点C坐标为(0,﹣1) ∴OA=OC, ∴∠OAC=45°, ∴∠BMC=2∠OAC=90° 又∵BC=  , ,∴MB=MC= 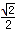 BC BC∴ 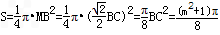 ; ;(3)如图,∵△ABC∽△APB, ∴∠PAB=∠BAC=∠45°, 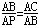 过点P作PD⊥x轴,垂足为D,连接PA、PB 在Rt△PDA中, ∵∠PAB=∠APD=45°, ∴PD=AD 设点P坐标为(x,x+1), ∵点P在抛物线上 ∴ 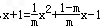 , ,即x2+(1﹣2m)x﹣2m=0, 解得x1=﹣1,x2=2m, ∴P1(2m,2m+1),P2(﹣1,0)(不合题意,舍去) 此时AP= 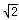 PD=(2m+1) PD=(2m+1) , ,又由 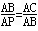 ,得AC·AP=AB2 ,得AC·AP=AB2则 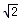 (2m+1) (2m+1)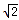 =(m+1)2, =(m+1)2,整理,得m2﹣2m﹣1=0 解得 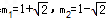 (舍去), (舍去),m的值是m= 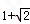 (只取正值)。 (只取正值)。 |
 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 与x轴的另一个交点为E.
与x轴的另一个交点为E.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| c | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com