
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为
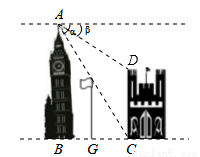
A.20米 B.10 米 C.15
米 C.15 米 D.5
米 D.5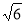 米
米
科目:初中数学 来源:2014-2015学年浙江省温州市升学考试适应性数学试卷(解析版) 题型:选择题
如图,已知正方形ABCD的边长为1,分别以顶点A,B,C,D为圆心,1为半径画弧,四条弧交于点E,F,G,H,则图中阴影部分的外围周长为( )
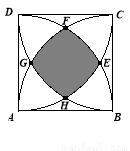
A.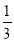
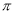 B.
B.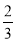
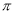 C.
C.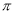 D.
D.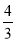
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省枣庄市中考模拟数学试卷(解析版) 题型:填空题
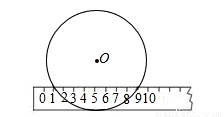
当宽为2cm的刻度尺的一边与圆相切时,另一边与图的两个交点处的度数如图,那么该圆的半径为 cm.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市沂水县九年级一轮模拟考试数学试卷(解析版) 题型:解答题
倡导研究性学习方式,着力教材研究,习题研究,是学生跳出题海,提高学习能力和创新能力的有效途径.下面是一案例,请同学们认真阅读、研究,完成“类比猜想”的问题.
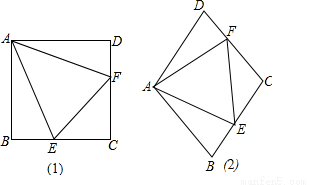
习题 如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°-45°=45°=∠EAF,又∵AE′=AE,AF=AF
∴△AE′F≌△AEF(SAS)∴EF=E′F=DE′+DF=BE+DF.
类比猜想:
(1)请同学们研究:如图(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?请说明理由.
(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF=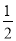 ∠BAD时,EF=BE+DF吗?请说明理由.
∠BAD时,EF=BE+DF吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市沂水县九年级一轮模拟考试数学试卷(解析版) 题型:填空题
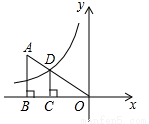
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=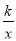 的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为_______.
的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为_______.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市沂水县九年级一轮模拟考试数学试卷(解析版) 题型:选择题
为了节省空间,家里的饭碗一般是摞起来存放的.如果6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,那么11只饭碗摞起来的高度更接近
A.21cm B.22cm C.23cm D.24cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市蒙阴县九年级一轮模拟考试数学试卷(解析版) 题型:解答题
已知抛物线y=ax2+bx+c经过 (-1,0),
(-1,0), (2,0),
(2,0), (0,2)三点.
(0,2)三点.

(1)求这条抛物线的解析式;
(2)如图①,点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标;
(3)如图②,设线段AC的垂直平分线交x轴于点E,垂足为D,M为抛物线的顶点,那么在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市蒙阴县九年级一轮模拟考试数学试卷(解析版) 题型:选择题
如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )
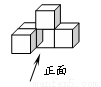
A.主视图的面积为5 B.左视图的面积为3
C.俯视图的面积为3 D.三种视图的面积都是4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市莒南县九年级一轮模拟考试数学试卷(解析版) 题型:填空题
如果一个数的平方等于-1,记作i2=-1,这个数叫做虚数单位.形如a+bi(a,b为有理数)的数叫复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
如:(2+i)+(3-5i)=(2+3)+(1-5)i=5-4i,
(5+i)×(3-4i)=5×3+5×(-4i)+i×3+i×(-4i)=15-20i+3i-4×i2=15-17i-4×(-1)=19-17i.
请根据以上内容的理解,利用以前学习的有关知识将(1+i)(1-i)化简结果为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com