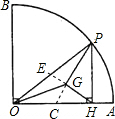
解:(1)当然是GH不变.
延长HG交OP于点E,
∵G是△OPH的重心,
∴GH=

EH,
∵PO是半径,它是直角三角形OPH的斜边,它的中线等于它的一半;
∴EH=

OP
∴GH=

(

OP)=

(

×6)=2;
(2)延长PG交OA于C,则y=

×PC.
我们令OC=a=CH,
在Rt△PHC中,PC=
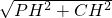
=

,
则y=

×

;
在Rt△PHO中,有OP
2=x
2+(2a)
2=6
2=36,
则a
2=9-

,
将其代入y=

×

得y=

×
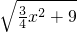
=
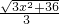
(0<x<6);
(3)如果PG=GH,则y=GH=2,
解方程:x=0,
那GP不等于GH,则不合意义;
如果,PH=GH=2则可以解得:x=2;
如果,PH=PG,则x=y代入可以求得:x=

,
综合上述线段PH的长是

或2.
分析:(1)由题意可知:重心是三角形中线交点,它把中线分为1:2的比例,如果中线长度不变,题中的三线段长度也不变.在直角三角形OHP中PO是直角三角形OPH的斜边,也是半径是保持不变的所以线段GH保持不变;则根据直角三角形中斜边的中线是斜边的一半可以求得OP中线的长度,进而求得GH的长度;
(2)延长PG交OA于C,则y=

×PC;分别再直角三角形OPh和直角三角形PHC中运用两次勾股定理即可以求出y关于x的函数解析式;
(3)分别讨论GH=PG,GH=PH,PH=PG这三种情况,根据(2)中的解析式可以分别求得x的值.
点评:本题考查了重心的概念以及直角三角形与等腰三角形的性质.综合性比较强,有一定的难度.

 心为G.
心为G. EH,
EH, OP
OP (
( OP)=
OP)= (
( ×6)=2;
×6)=2; ×PC.
×PC.
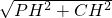 =
= ,
, ×
× ;
; ,
, ×
× 得y=
得y= ×
×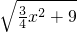 =
=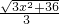 (0<x<6);
(0<x<6); ,
, 或2.
或2. ×PC;分别再直角三角形OPh和直角三角形PHC中运用两次勾股定理即可以求出y关于x的函数解析式;
×PC;分别再直角三角形OPh和直角三角形PHC中运用两次勾股定理即可以求出y关于x的函数解析式;

 备战中考寒假系列答案
备战中考寒假系列答案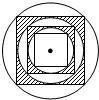 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( ) 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是