
抛物线![]() 的顶点在直线
的顶点在直线![]() 上,过点F
上,过点F![]() 的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥
的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥![]() 轴于点A,NB⊥
轴于点A,NB⊥![]() 轴于点B.
轴于点B.
(1)(3分)先通过配方求抛物线的顶点坐标(坐标可用含![]() 的代数式表示),再求
的代数式表示),再求![]() 的值;
的值;
(2)(3分)设点N的横坐标为![]() ,试用含
,试用含![]() 的代数式表示点N的纵坐标,并说明NF=NB;
的代数式表示点N的纵坐标,并说明NF=NB;
(3)(3分)若射线NM交![]() 轴于点P,且PA×PB=
轴于点P,且PA×PB=![]() ,求点M的坐标.
,求点M的坐标.

 (1)
(1)![]() …1分
…1分
∴顶点坐标为(-2 , ![]() )…………………2分
)…………………2分
∵顶点在直线![]() 上,
上,
∴-2+3=![]() ,得
,得![]() =2…………………3分
=2…………………3分
(2)∵点N在抛物线上,
∴点N的纵坐标为![]() …………………………4分
…………………………4分
即点N(![]() ,
,![]() )
)
过点F作FC⊥NB于点C,
在Rt△FCN中,FC=![]() +2,NC=NB-CB=
+2,NC=NB-CB=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() ………………………………………………5分
………………………………………………5分
而![]() =
=![]() =
=![]()
∴![]() =
=![]() ,NF=NB………………………………………………………………………6分
,NF=NB………………………………………………………………………6分
(3)连结AF、BF
由NF=NB,得∠NFB=∠NBF,由(2)的结论知,MF=MA,∴∠MAF=∠MFA,∵MA⊥![]() 轴,NB⊥
轴,NB⊥![]() 轴,∴MA∥NB,∴∠AMF+∠BNF=180°
轴,∴MA∥NB,∴∠AMF+∠BNF=180°
∵△MAF和△NFB的内角总和为360°,∴2∠MAF+2∠NBF=180°,∠MAF+∠NBF=90°,
∵∠MAB+∠NBA=180°,∴∠FBA+∠FAB=90°又∵∠FAB+∠MAF=90°
∴∠FBA=∠MAF=∠MFA
又∵∠FPA=∠BPF,∴△PFA∽△PBF,∴![]() ,
,![]() =
=![]() ……………7分
……………7分
过点F作FG⊥![]() 轴于点G,在Rt△PFG中,PG=
轴于点G,在Rt△PFG中,PG=![]() =
=![]() ,∴PO=PG+GO=
,∴PO=PG+GO=![]() ,
,
∴P(-![]() , 0)
, 0)
设直线PF:![]() ,把点F(-2 , 2)、点P(-
,把点F(-2 , 2)、点P(-![]() , 0)代入
, 0)代入![]() 解得
解得![]() =
=![]() ,
,![]() =
=![]() ,∴直线PF:
,∴直线PF:![]() ……………………………………………………8分
……………………………………………………8分
解方程![]() ,得
,得![]() =-3或
=-3或![]() =2(不合题意,舍去)
=2(不合题意,舍去)
当![]() =-3时,
=-3时,![]() =
=![]() ,∴M(-3 ,
,∴M(-3 ,![]() )……………………………9分
)……………………………9分


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
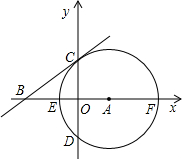 ,与y轴交于C、D两点,过C点作⊙A的切线BC交x轴于B.
,与y轴交于C、D两点,过C点作⊙A的切线BC交x轴于B.
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 D两点,过C点作⊙A的切线BC交x轴于B.
D两点,过C点作⊙A的切线BC交x轴于B.
| ||
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 D两点,过C点作⊙A的切线BC交x轴于B.
D两点,过C点作⊙A的切线BC交x轴于B. x+2
x+2 上,求此抛物线的解析式;
上,求此抛物线的解析式;查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州萧山回澜初中九年级12月阶段性测试数学试卷(解析版) 题型:选择题
已知:二次函数 ,下列说法中错误的个数是( )
,下列说法中错误的个数是( )
①若图象与 轴有交点,则
轴有交点,则 .
.
②若该抛物线的顶点在直线 上,则
上,则 的值为
的值为 .
.
③当 时,不等式
时,不等式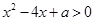 的解集是
的解集是 .
.
④若将图象向上平移1个单位,再向左平移3个单位后过点 ,则
,则 .
.
⑤若抛物线与x轴有两个交点,横坐标分别为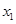 、
、 ,则当x取
,则当x取 时的函数值与x取0时的函数值相等.
时的函数值与x取0时的函数值相等.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2008-2009学年安徽省芜湖市南陵县实验初中九年级(上)第四次月考数学试卷(解析版) 题型:解答题
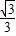 x+2
x+2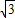 上,求此抛物线的解析式;
上,求此抛物线的解析式;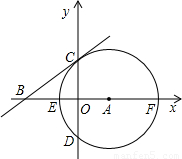
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com