

|
|
| 1 |
| 3 |
| s |
| SĄũAOB |
| OC |
| AO |
| s |
| 9 |
| 1 | ||
3
|
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 4 |

| 36 |
| 5 |
| 9 |
| 4 |
| 36 |
| 5 |
| 9 |
| 4 |
| 99 |
| 20 |
| x2 |
| 5 |
| (x-3)2 |
| 4 |
| x2 |
| 5 |
| (x-3)2 |
| 4 |
| 21 |
| 20 |
| 27 |
| 2 |
| 153 |
| 4 |
| 21 |
| 20 |
| 45 |
| 7 |
| 36 |
| 7 |
| 45 |
| 7 |
| 36 |
| 7 |
| 45 |
| 7 |
| 36 |
| 7 |
|
| 9 |
| 5 |
| 99 |
| 20 |
| 45 |
| 7 |
| 36 |
| 7 |
| 63 |
| 16 |
| 45 |
| 7 |
| 36 |
| 7 |


 ÔÄķÁŋėģĩÏĩÁÐīð°ļ
ÔÄķÁŋėģĩÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢš―âīðĖâ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢš―âīðĖâ

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢš―âīðĖâ
| 1 |
| 2 |
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢšĩĨŅĄĖâ
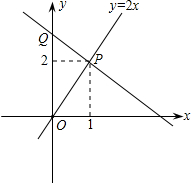
| AĢŪ3x-2y+3.5=0 | BĢŪ3x-2y-3.5=0 |
| CĢŪ3x-2y+7=0 | DĢŪ3x+2y-7=0 |
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢš―âīðĖâ
| 5 |
| 16 |

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢš―âīðĖâ
| 1 |
| 2 |
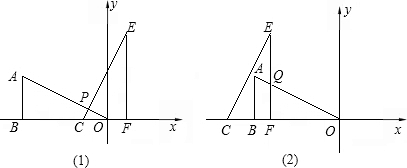
 DΊֹūķŨũĄŅA―ŧCDÓÚFĢŽFAĩÄŅÓģĪÏß―ŧĄŅAÓÚEĢŽ―ŧxÖáÓÚBĢŪ
DΊֹūķŨũĄŅA―ŧCDÓÚFĢŽFAĩÄŅÓģĪÏß―ŧĄŅAÓÚEĢŽ―ŧxÖáÓÚBĢŪēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢš―âīðĖâ
| 3 |
| 3 |

ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšģõÖÐĘýŅ§ ĀīÔīĢšēŧÏę ĖâÐÍĢš―âīðĖâ
| 33 |
| 2 |

ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com