
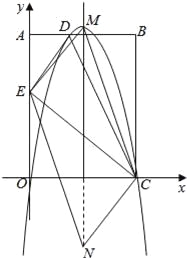
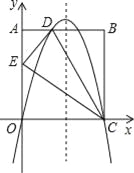
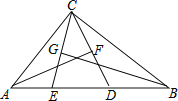
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x(2)t=
x(2)t=![]() 或
或![]() (3)①M1(4,
(3)①M1(4, ![]() ),N1(4,﹣
),N1(4,﹣![]() );②M2(12,﹣32),N2(4,﹣26);③M3(﹣4,﹣32),N3(4,﹣38).
);②M2(12,﹣32),N2(4,﹣26);③M3(﹣4,﹣32),N3(4,﹣38).
【解析】试题分析:(1)根据折叠图形的轴对称性,△CED、△CBD全等,首先在Rt△CEO中求出OE的长,进而可得到AE的长;在Rt△AED中,AD=AB﹣BD、ED=BD,利用勾股定理可求出AD的长.进一步能确定D点坐标,利用待定系数法即可求出抛物线的解析式.
(2)由于∠DEC=90°,首先能确定的是∠AED=∠OCE,若以P、Q、C为顶点的三角形与△ADE相似,那么∠QPC=90°或∠PQC=90°,然后在这两种情况下,分别利用相似三角形的对应边成比例求出对应的t的值.
(3)由于以M,N,C,E为顶点的四边形,边和对角线都没明确指出,所以要分情况进行讨论:
①EC做平行四边形的对角线,那么EC、MN必互相平分,由于EC的中点正好在抛物线对称轴上,所以M点一定是抛物线的顶点;
②EC做平行四边形的边,那么EC、MN平行且相等,首先设出点N的坐标,然后结合E、C的横、纵坐标差表示出M点坐标,再将点M代入抛物线的解析式中,即可确定M、N的坐标.
试题解析:方法一:
解:(1)∵四边形ABCO为矩形,
∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.
由题意,△BDC≌△EDC.
∴∠B=∠DEC=90°,EC=BC=10,ED=BD.
由勾股定理易得EO=6.
∴AE=10﹣6=4,
设AD=x,则BD=ED=8﹣x,由勾股定理,得x2+42=(8﹣x)2,
解得,x=3,∴AD=3.
∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),O(0,0)
∴![]() ,
,
解得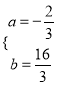
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x.
x.
(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,
∴∠DEA=∠OCE,
由(1)可得AD=3,AE=4,DE=5.
而CQ=t,EP=2t,∴PC=10﹣2t.
当∠PQC=∠DAE=90°,△ADE∽△QPC,
∴![]() ,
,
即![]() ,
,
解得t=![]() .
.
当∠QPC=∠DAE=90°,△ADE∽△PQC,
∴![]() ,
,
即![]() ,
,
解得t=![]() .
.
∴当t=![]() 或
或![]() 时,以P、Q、C为顶点的三角形与△ADE相似.
时,以P、Q、C为顶点的三角形与△ADE相似.
(3)假设存在符合条件的M、N点,分两种情况讨论:
①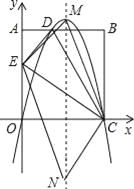
EC为平行四边形的对角线,由于抛物线的对称轴经过EC中点,若四边形MENC是平行四边形,那么M点必为抛物线顶点;
则:M(4, ![]() );而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣
);而平行四边形的对角线互相平分,那么线段MN必被EC中点(4,3)平分,则N(4,﹣![]() );
);
②EC为平行四边形的边,则EC∥MN,EC=,MN设N(4,m),则M(4﹣8,m+6)或M(4+8,m﹣6);
将M(﹣4,m+6)代入抛物线的解析式中,得:m=﹣38,此时 N(4,﹣38)、M(﹣4,﹣32);
将M(12,m﹣6)代入抛物线的解析式中,得:m=﹣26,此时 N(4,﹣26)、M(12,﹣32);
综上,存在符合条件的M、N点,且它们的坐标为:
①M1(﹣4,﹣32),N1(4,﹣38);②M2(12,﹣32),N2(4,﹣26);③M3(4, ![]() ),N3(4,﹣
),N3(4,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE.(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
A.至少有1个球是黑球
B.至少有1个球是白球
C.至少有2个球是黑球
D.至少有2个球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会准备调查七年级叙述参加“绘画类”、“书法类”、“乐器类”四类校本课程的人数,在全校进行随机抽样调查,并根据收集的数据绘制了如图两幅统计图(信息尚不完整),请根据图中提供的信息,解答下面的问题: 
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中乐器部分的圆心角的度数;
(3)如果该校共有1000名学生参加这4个课外兴趣小组,而每个教师最多只能辅导本组的25名学生,估计书法兴趣小组至少需要准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天上一颗颗闪烁的星星给我们以“_____”的形象;中国武术中有“枪扎一条线,棍扫一大片”的说法,这句话给我们以“_____”的形象;宾馆里旋转的大门给我们以“_____”的形象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90°;④∠4+∠5=180°,其中正确的个数是( ) 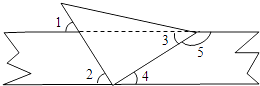
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com