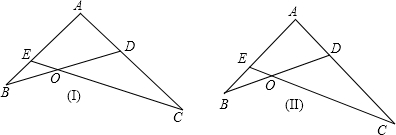
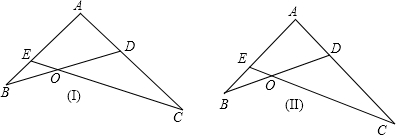
证明:题目I,∵∠B=∠C,∠BAD=∠EAC,
∴△ABD∽△ACE,
∴
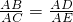
;
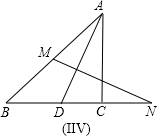
题目II:
∵

,
∴
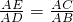
,
∵∠BAD=∠EAC,
∴△ADB∽△AEC,
∴∠B=∠C,
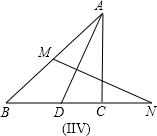
∵∠BOE=∠COD,
∴△BOE∽△COD,
∴
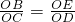
,OB•OD=OC•OE;
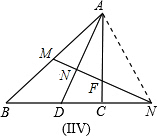
题目III:如图,连接AN,
∵M是AD中点,MN⊥AD交BC的延长线于N,
∴AN=DN,∠ADN=∠DAN,∠ANM=∠DNM,
在△ABD中,
∠AND=∠B+∠MAD,
∵AD是∠BAC的平分线,
∴∠CAD=∠MAD,
∵∠DAN=∠DAC+∠CAN,
∴∠CAN=∠B,
又∵∠ANM=∠DNM,
∴△ANF∽△BNE,
∴
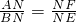
.
∵AD是∠BAC的平分线,MN⊥AD,
∴∠AEF=∠AFE,
∵∠ANE=∠DNE,
∴△ANE∽△CNF,
∴
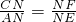
,
∴
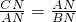
,
∵AN=DN,
∴DN
2=BN•CN.
分析:(1)根据已知条件求出△ABD∽△ACE,再根据相似三角形的对应边成比例即可解答;
(2)先根据已知条件可得出

=

,再根据∠BAD=∠EAC可求出△ADB∽△AEC,再由相似三角形的对应角相等可求出∠B=∠C,由相似三角形的判定定理可求出△BOE∽△COD,再根据相似三角形的对应边成比例解答即可;
(3)连接AN,根据M是AD中点,MN⊥AD可知AN=DN,由等腰三角形三线合一的特点可知∠ANE=∠DNE,
利用角平分线及三角形内角与外角的关系可知∠CAN=∠B,利用相似三角形的判定定理可知△BOE∽△COD,根据相似三角形的性质及角平分线判定定理可得△ANE∽△CNF,再由相似三角形的对应边成比例即可得出结论.
点评:此题比较复杂,涉及到相似三角形的判定定理及性质、等腰三角形的判定定理及性质、角平分线的性质,涉及面较广,难度较大.

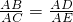 ;
; ,试说明OB•OD=OC•OE;
,试说明OB•OD=OC•OE; 证明:题目I,∵∠B=∠C,∠BAD=∠EAC,
证明:题目I,∵∠B=∠C,∠BAD=∠EAC,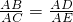 ;
; ,
,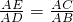 ,
,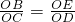 ,OB•OD=OC•OE;
,OB•OD=OC•OE;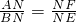 .
.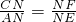 ,
,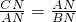 ,
, =
= ,再根据∠BAD=∠EAC可求出△ADB∽△AEC,再由相似三角形的对应角相等可求出∠B=∠C,由相似三角形的判定定理可求出△BOE∽△COD,再根据相似三角形的对应边成比例解答即可;
,再根据∠BAD=∠EAC可求出△ADB∽△AEC,再由相似三角形的对应角相等可求出∠B=∠C,由相似三角形的判定定理可求出△BOE∽△COD,再根据相似三角形的对应边成比例解答即可;