Question

若AB、AC是⊙O的弦，AB、AC的长分别是⊙O的内接正八边形和正二十四边形的边长，则BC的长是⊙O的内接正    边形的长．

Answer 1

【答案】分析：根据已知画出图象，利用C点与A，B不同的位置关系得出答案即可．
解答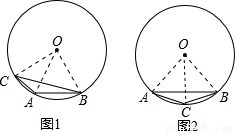：解：如图所示：
∵AB、AC的长分别是⊙O的内接正八边形和正二十四边形的边长，
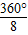
∴∠COA==15°，∠AOB==45°，
∴∠COB=15°+45°=60°，
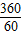
=6，
∵AB、AC的长分别是⊙O的内接正八边形和正二十四边形的边长，
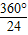
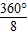
∴∠COA==15°，∠AOB==45°，
∴∠COB=45°-15°=30°，
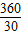
=12，
故BC的长是⊙O的内接正六或十二边形的长．
故答案为：六或十二．
点评：此题主要考查了正多边形和圆的有关计算，根据已知得出正多边形中心角的度数是解题关键．