
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.
(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°;
①求∠OCE的度数. ②若⊙O的半径为 ![]() ,求线段CF的长.
,求线段CF的长.

【答案】(1)答案见解析;(2)①45°;②4
【解析】试题分析:
(1) 要证AC平分∠DAO,就是要证∠DAC=∠OAC. 观察图形易知,在等腰三角形AOC中,∠OAC=∠OCA. 根据切线的性质定理可知,OC⊥CD,结合已知条件易知AD∥OC. 利用内错角的相等关系,可以证明∠OCA=∠DAC,进而证明AC平分∠DAO.
(2) 由AD∥OC可知,∠DAO=∠EOC. 在△COE中,利用已知条件和三角形内角和,可以求得∠OCE的度数. 观察图形可知,线段CF是⊙O的一条弦. 考虑利用垂径定理的相关知识求解线段CF的长. 过圆心O作弦CF的垂线,垂足设为G,则点G为弦CF的中点. 根据垂直关系和∠OCE的度数不难发现△OGC是等腰直角三角形. 结合已知条件,在△OGC中利用勾股定理可以求得线段CG的长,进而得到线段CF的长.
试题解析:
(1) 证明:
∵直线CD与⊙O相切,点C在⊙O上,
∴OC⊥CD,
∵AD⊥CD,OC⊥CD,
∴AD∥OC,
∴∠DAC=∠OCA.
∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC,
∴AC平分∠DAO.
(2) ①∵AD∥OC,∠DAO=105°,
∴∠EOC=∠DAO=105°,
∵∠E=30°,
∴在△COE中,∠OCE=180°-∠EOC-∠E=180°-105°-30°=45°.
②
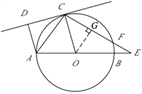
如图,过点O作OG⊥CE,垂足为G.
根据垂径定理,得FG=CG.
∵OG⊥CE,∠OCE=45°,即∠OCG=45°,
∴在Rt△OGC中,∠COG=∠OCG=45°,
∴CG=OG.
∵⊙O的半径为![]() ,
,
∴OC=![]() ,
,
∴在Rt△OGC中, ![]() .
.
∴CG=2.
∵FG=CG,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了解全校七年级300名学生的视力情况,从中抽查了50名学生的视力情况.这个问题中,下面说法正确的是( )
A. 300名学生是总体B. 样本容量是50
C. 50名学生是所抽取的一个样本D. 每名学生是个体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】代数式x3-4x2+4x分解因式的结果为 ( )
A. x(x2-4x+4) B. x(x-2)2 C. x(x+2)2 D. x(x+2)(x-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年12月27日,苏州环古城河健康步道全线开通了.环古城河健身步道全程15 500m,沿护城河内岸环绕苏州古城.将数据15500用科学记数法可表示为( )
A.0.155×104
B.0.155×105
C.1.55×104
D.1.55×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个月内,小丽的体重增长﹣1千克,意思就是这个月内( )
A. 小丽的体重减少﹣1千克 B. 小丽的体重增长1千克
C. 小丽的体重减少1千克 D. 小丽的体重没变化
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com