在Rt△ABC中,∠C=90°,AC=5,BC=12,若以C为圆心,以5为半径作⊙O,则点A在⊙C________,点B在⊙C________;若以AB为直径作⊙D,则点C在⊙D________.
上 外 上
分析:用勾股定理求出直角三角形的斜边,再根据直角三角形斜边上的中线等于斜边的一半得到CD的长,然后由点到圆心的距离与圆的半径大小的比较,确定点的位置.
解答:
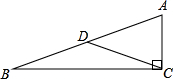
解:如图:因为AC=5,所以以C为圆心,5为半径时,点A在⊙C上.
又因为BC=12>5,所以点B在⊙C外.
在Rt△ABC中,AB=

=

=13,
以AB为直径作⊙D,则D为AB的中点,所以AD=BD=CD=6.5.所以点C在⊙D上.
故答案分别是:点A在⊙C上,点B在⊙C外,点C在⊙D上.
点评:本题考查的是点与圆的位置关系,根据题意可以求出AB和CD的长,然后由点到圆心的距离与圆半径比较,确定点的位置.
