
如图1所示:AM∥DN,AE、DE分别平分∠MAD和∠AND,并交于E点. 过点E的直线分别交AM、DN于B、C.
(1)如图2,当点B、C分别位于点AD的同侧时,猜想AD、AB、CD之间的存在的数量关系:_______________________________.
(2)试证明你的猜想.
(3)若点B、C分别位于点AD的两侧时,试写出AD、AB、CD之间的关系,并选择一个写出证明过程。


(1)AD=AB+CD………………………………1分
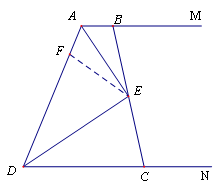 (2)证明:在AD上截取AF=AB,连接EF.
(2)证明:在AD上截取AF=AB,连接EF.
∵AE平分∠BAD
∴∠BAE=∠FAE
在△ABE和△AFE中
![]() AB=AF
AB=AF
∠BAE=∠FAE
AE=AE
∴△ABE≌△AFE………………………………2分
∴∠ABC=∠AFE
∵ AB∥CD
∴∠ABC+∠BCD=180°
又∵∠AFE+∠DFE=180°
∴∠DFE=∠C
∵DE平分∠ADC
∴∠ADE=∠CDE
在△FDE和△CDE中
![]() ∠DFE=∠C
∠DFE=∠C
∠ADE=∠CDE
DE=DE
∴△FDE≌△CDE ……………………………3分
∴DF=CD
∴AF+DF=AB+CD
即AD=AB+CD………………………………….4分
(3)证明:
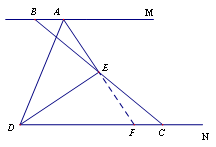 第一种情况:当点B位于点A左侧,点C位于点D右侧时,DC=AD+AB. …………………5分
第一种情况:当点B位于点A左侧,点C位于点D右侧时,DC=AD+AB. …………………5分
在CD上截取DF=AD,连接EF.
∵DE平分∠ADC
∴∠ADE=∠CDE
在△ADE和△FDE中
![]() DA=DF
DA=DF
∠ADE=∠CDE
DE=DE
∴△ADE≌△FDE……………………………….6分
∴EA=EF
∠DAE=∠DFE
∵AE平分∠DAM
∴∠DAE=∠EAM
∴∠DFE=∠EAM
又∵∠BAE+∠EAM=180°
∠DFE+∠CFE=180°
∴∠BAE=∠CF![]() E
E
∵AM∥DN
∴∠ABC=∠BCD
在△BAE和△CFE中
![]() ∠BAE=∠CFE
∠BAE=∠CFE
∠ABC=∠BCD
EA=EF
∴△BAE≌△CFE
∴AB=FC
∵DC=DF+FC
∴DC=AD+AB………………………………………..7分
第二种情况:当点B位于点A右侧,点C位于点D左侧时,AB=AD+CD.……………….5分.
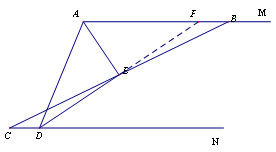 在AB上截
在AB上截![]() 取AF=AD,连接EF
取AF=AD,连接EF
∵AE平分∠BAD
∴∠BAE=∠DAE
在△ADE和△AEF中
![]() AF=AD
AF=AD
∠BAE=∠DAE
AE=AE
∴△AEF≌△AED………………………………………………6分
∴EF=ED
∴∠AFE=∠ADE
∵DE平分∠ADN
∴∠ADE=∠EDN
∴∠AFE=∠EDN
又∵∠AFE+∠BFE=180°
∠EDN+∠EDC=180°
∴∠BFE=∠EDC
∵AM∥DN
∴∠ABC=∠BCD
在△BEF和△CED中
![]() ∠BFE=∠EDC
∠BFE=∠EDC
∠ABC=∠BCD
DE=EF
∴△BFE≌△CDE
∴CD=BF
∵AB=AF+FB
∴AB=AD+C![]() D…………………………………………………7分
D…………………………………………………7分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 21 |
| 2 |
| 3 |
| 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com