
分析 (1)题意即可得到结论;
(2)根据题意列方程即可得到结论;
(3)t秒后,数轴上A点、B点表示的数为a、b,则线段AB的中点M表示的数为$\frac{a+b}{2}$,于是得到方程,解方程即可得到结论.
解答 解:(1)运动开始前,A、B两点的距离为|-40-20|=60;线段AB的中点M所表示的数为$\frac{1}{2}$(-40+20)=-10;
故答案为:60,-10;
(2)3t+2t=60,
∴t=12,
∴3t=36,2t=24,
∴-40+36=-4,
∴相遇点所表示的数是-4;
(3)t秒后,数轴上A点、B点表示的数为a、b,
则线段AB的中点M表示的数为$\frac{a+b}{2}$,
∴$\frac{a+b}{2}$=-5,
∴3t+2t=60-10=50,
∴t=10,
∴当t为10时,线段AB的中点M表示的数为-5.
点评 此题考查了数轴,弄清题意是解本题的关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
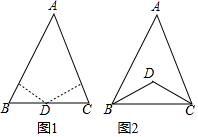 已知:点D到△ABC的两边AB、AC所在直线的距离相等,且DB=DC.
已知:点D到△ABC的两边AB、AC所在直线的距离相等,且DB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com