Question

【题目】如图，△ABC和△CDE都是等边三角形，则下列结论不成立的是（ ）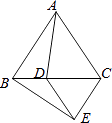
A.∠BDE=120°
B.∠ACE=120°
C.AB=BE
D.AD=BE

Answer 1

【答案】B
【解析】解：∵△CDE都是等边三角形， ∴∠CDE=60°，
∴∠BDE=180°﹣∠CDE=120°，故A正确；
∵△ABC和△CDE都是等边三角形，
∴∠ACB=60°，∠DCE=60°，
∴∠ACE=∠ACB+∠DCE=60°+60°=120°，故B正确；
∵△ABC和△CDE都是等边三角形，
∴AC=BC，EC=DC，∠ACD=∠BCE=60°．
在△ACD和△BCE中，
，
∴△ACD≌△BCE（SAS），
∴AD=BE．故D正确；
∵△ABD与△EBD不全等，
∴AB≠BE．
故选：B．
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案，需要熟知等边三角形的三个角都相等并且每个角都是60°．