
【题目】为了估计鱼塘中成品鱼(个体质量在0.5 kg及以上,下同)的总质量,先从鱼塘中捕捞50条成品鱼,称得它们的质量如下表:

然后做上记号再放回鱼塘中,过几天又捕捞了100条成品鱼,发现其中2条带有记号.
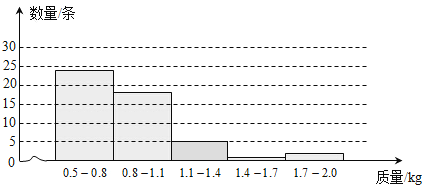
(1)请根据表中数据补全下面的直方图(各组中数据包括左端点不包括右端点);

(2)根据图中数据分组,估计从鱼塘中随机捕一条成品鱼,其质量落在哪一组的可能性最大?
(3)根据图中数据分组,估计鱼塘里质量中等的成品鱼,其质量落在哪一组内?
(4)请你用适当的方法估计鱼塘中成品鱼的总质量(精确到1 kg).
【答案】(1)补图略;(2)其质量落在0.5~0.8 kg这一组的可能性最大;(3)质量落在0.8~1.1 kg这一组内;(4)平均数2260kg.
【解析】(1)由函数图象可以得出1.1-1.4的有5条,补全图形,得

(2)由题意,得
0.5-0.8的频率为:24÷50=0.48,
0.8-1.1的频率为:18÷50=0.36,
1.1-1.4的频率为:5÷50=0.1,
1.4-1.7的频率为:1÷50=0.02,
1.7-2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5-0.8 kg的可能性最大.
(3)这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0
∴鱼塘里质量中等的成品鱼,其质量落在0.8-1.1 kg内;
(4)设鱼塘中成品鱼的总质量为x,由题意,得
50:x=2:100,解得:x=2500.
∵2500×0.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×2500.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×250=2260,
∴估计鱼塘中成品鱼的总质量为2260kg.
分析:(1)由函数图象可以得出1.1-1.4的有5条,就可以补全直方图;
(2)分别求出各组的频率,就可以得出结论;
(3)由这组数据的个数为50,就可以得出第25个和第26个数的平均数就可以得出结论;
(4)设鱼塘中成品鱼的条数为x,根据作记号的鱼50:x=2:100建立方程求出其解即可.
详解:(1)由函数图象可以得出1.1-1.4的有5条,补全图形,得:
(2)由题意,得
0.5-0.8的频率为:24÷50=0.48,
0.8-1.1的频率为:18÷50=0.36,
1.1-1.4的频率为:5÷50=0.1,
1.4-1.7的频率为:1÷50=0.02,
1.7-2.0的频率为:2÷50=0.04.
∵0.48>0.36>0.1>0.04>0.02.
∴估计从鱼塘中随机捕一条成品鱼,其质量落在0.5-0.8的可能性最大;
(3)这组数据的个数为50,就可以得出第25个和第26个数分别是1.0,1.0,
∴(1.0+1.0)÷2=1.0,
鱼塘里质量中等的成品鱼,其质量落在0.8-1.1内;
(4)设鱼塘中成品鱼的条数为x,由题意,得:
50:x=2:100,
解得:x=2500.
2500×0.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×2500.5×1+0.6×8+0.7×15+1×18+1.2×5+1.6×1×250=2260kg.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知α,β是关于x的一元二次方程x2+ (2m+3)x+m2=0 的两个不相等的实数根,且满足![]() = -1,则m的值是( ).
= -1,则m的值是( ).
A. 3或 -1 B. 3 C. -1 D. -3 或 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①△ABF≌△ADF;②S△ADF=2S△CEF;③tan∠EBF=![]() ;④S△ABF=4S△BEF,其中正确结论的个数是( )
;④S△ABF=4S△BEF,其中正确结论的个数是( )
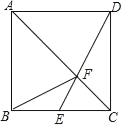
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进了甲、乙两种型号的中性笔共4000支,甲型号中性笔进价是3元/支,乙型号中性笔进价是7元/支,购进两种型号的中性笔共用去16000元.
(1)求甲、乙两种型号的中性笔各购进了多少支;
(2)为使每支乙型号中性笔的利润是甲型号的1.8倍,且保证售完这4000支中性笔的利润不低于7200元,求每支甲型号中性笔的售价至少是多少元.(注:利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角.关于这七个角的度数关系,下列何者正确( )
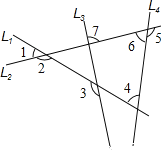
A. ∠2=∠4+∠7 B. ∠3=∠1+∠6 C. ∠1+∠4+∠6=180° D. ∠2+∠3+∠5=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
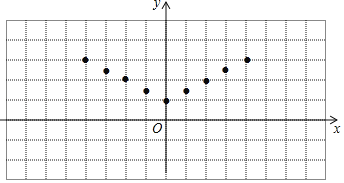
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同的棱长为![]() 的小正方体堆成一个几何体,如下图所示.
的小正方体堆成一个几何体,如下图所示.
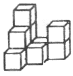



(1)该几何体是由 个小正方体组成,请画出它的主视图、左视图、俯视图(网格中所画的图形要画出各个正方形边框并涂上阴影).
(2)如果在这个几何体露在外面的表面喷上黄色的漆,每平方厘米用2克,则共需 克漆.
(3)这个几何体上,再添加一些相同的小正方体并保持这个几何体的俯视图和左视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
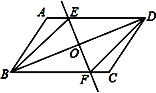
【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com