
 如图,△ABC中,∠ACB=90°,AC=BC,AD是中线,点E与点C关于AD对称,CE交AD于F,连接BE.
如图,△ABC中,∠ACB=90°,AC=BC,AD是中线,点E与点C关于AD对称,CE交AD于F,连接BE.分析 (1)根据轴对称的性质可得CF=EF,AF⊥CE,再根据中线的定义可得CD=DB,然后判断出DF是△BCF的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求出DF∥BE,根据两直线平行,同位角相等可得∠E=∠CFD;
(2)根据同角的余角相等求出∠CAF=∠BCE,然后利用“角角边”证明△ACF和△CBE全等,根据全等三角形对应边相等可得CF=EB,再根据CF=EF等量代换即可得证.
解答 (1)解:∵点E与点C关于AD对称,
∴CF=EF,AF⊥CE,
∴∠CFD=90°,
∵AD是中线,
∴CD=DB,
∴DF是△BCF的中位线,
∴DF∥BE,
∵∠E=∠CFD=90°;
(2)证明:∵∠ACB=90°,
∴∠ACF+∠BCE=90°,
∵AF⊥CE,
∴∠CAF+∠ACF=90°,
∴∠CAF=∠BCE,
在△ACF和△CBE中,$\left\{\begin{array}{l}{∠CAF=∠BCE}\\{∠AFC=∠E=90°}\\{AC=BC}\end{array}\right.$,
∴△ACF≌△CBE(AAS),
∴CF=EB,
∵CF=EF,
∴EB=EF.
点评 本题考查了全等三角形的判定与性质,轴对称的性质,三角形的中位线平行于第三边并且等于第三边的一半,同角的余角相等的性质,(1)难点在于判断出DF是△BCF的中位线,(2)熟练掌握三角形全等的判定方法并确定出全等三角形是解题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
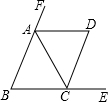 如图,在△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.
如图,在△ABC中,AB=AC,AD是△ABC外角的平分线,已知∠BAC=∠ACD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 零除以任何数都等于零 | |
| B. | 1除以一个数就等于乘这个数的倒数 | |
| C. | 一个不等于零的有理数除以它的相反数等于-1 | |
| D. | 两数相除,商一定小于被除数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届广东省东莞市堂星晨学校九年级第一次模拟数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:解答题
如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com