已知梯形两底角之和为90°，上底长为5，下底长11，则连接两底中点的线段长为 ．
【答案】
分析：过上底中点作两腰的平行线与下底相交得到直角三角形和两个平行四边形，再根据直角三角形斜边上的中线等于斜边的一半即可求解．
解答：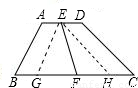
解：如图，过E作EG∥AB交BC于G，作EH∥CD交BC于H，
∴∠EGF=∠B，∠EHF=∠C，
∵∠B+∠C=90°，
∴∠EGF+∠EHF=90°，
∴∠GEH=90°，
∵点E、F分别是AD、BC的中点，
∴AE=ED=BG=CH，
∴GF=FH，
∵AD=5，BC=11，
∴GH=11-5=6，
∴EF=
GH=3．
点评：本题主要利用直角三角形斜边上的中线等于斜边的一半的性质，通过作平行线，把两底角之和为90°转化为三角形的两个内角是解题的关键．
