
 ��OB=4���ֽ�Rt��AOB����ֱ�Ƕ���O����ʱ�뷽����ת90��õ���COD����֪һ�����߾���C��D��B���㣮
��OB=4���ֽ�Rt��AOB����ֱ�Ƕ���O����ʱ�뷽����ת90��õ���COD����֪һ�����߾���C��D��B���㣮 �⣺��1���ߡ�COD�ա�AOB
�⣺��1���ߡ�COD�ա�AOB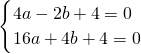
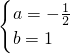

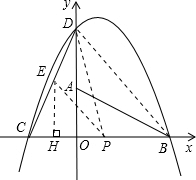 ��2����E��EH��x�ᣬ
��2����E��EH��x�ᣬ CP•OD-
CP•OD- CP•EH
CP•EH CP��OD-EH��
CP��OD-EH��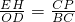
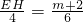
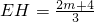

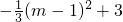
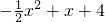 ����y=3
����y=3 ��x2=1-
��x2=1-
 ��0��Q2��-2-
��0��Q2��-2- ��0��
��0��
 ��x2=1-
��x2=1-
 ��0��Q4��4-
��0��Q4��4- ��0��
��0��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 9 | x |
 ���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ��
���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ��������
5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ���������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
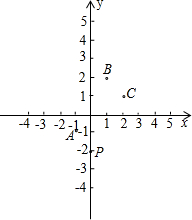 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ��
��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ
��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 BE��
BE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com