在△ABC中,经过重心G作线段DE∥BC交AB于D,交AC于E,则DE:BC=________.
2:3
分析:首先根据相似三角形的判定与性质得出

=

,再利用根据三角形的重心到顶点的距离是它到对边中点的距离的2倍,即可得出答案.
解答:连接AG并延长到BC边上一点F,
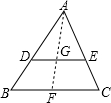
∵在△ABC中,经过重心G作线段DE∥BC交AB于D,交AC于E,
∴△ADE∽△ABC,△AGE∽△AFC,
∴

,

=

,
∴

=

,
∵AG=2GF,
∴

=

=

故答案为:2:3.
点评:此题主要考查了三角形重心的性质以及相似三角判定和性质,根据三角形相似得出

=

是解决问题的关键.
