Question

在四边形ABCD中，对角线AC⊥BD，那么依次连接四边形ABCD各边中点所得的四边形一定是（ ）
A．菱形
B．矩形
C．正方形
D．平行四边形

Answer 1

【答案】分析：利用三角形中位线定理可以推知四边形EFGH是平行四边形；然后由三角形中位线定理、已知条件“AC⊥BD”推知HE⊥HG；最后由矩形判定定理“有一内角为直角是平行四边形是矩形”可以证得?EFGH是矩形．
解答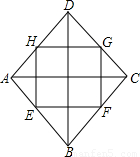：解：如图所示：AC⊥BD，点E、F、G、H分别是边AB、BC、CD、DA的中点；
∵在△DAC中，根据三角形中位线定理知，HG∥AC且HG=AC；
同理在△ABC中，EF∥AC且EF=AC，
∴HG∥EF∥AC，且HG=EF，
∴四边形EFGH是平行四边形；
同理，HE∥DB；
又∵AC⊥BD，
∴HE⊥HG，
∴?EFGH是矩形；
故选B．
点评：本题考查了三角形中位线定理、矩形的判定定理．三角形的中位线平行于第三边且等于第三边的一半．