解:(1)生产甲种配件的人数为300-x,平均每人每年创造的利润为m×(1+20%)万元,
所以调配后企业生产甲种配件的年利润为(300-x)(1+20%)m万元;
生产乙种配件的人数为x,平均每人每年创造的利润为1.54m,所以生产乙种配件的年利润为1.54mx万元;
(2)
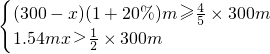
,
解得97

<x≤100,
∵x为正整数,
∴x可取98,99,100.
∴共有三种调配方案:
①202人生产甲种配件,98人生产乙种配件;
②201人生产甲种配件,99人生产乙种配件;
③200人生产甲种配件,100人生产乙种配件;
分析:(1)调配后企业生产甲种配件的年利润=生产甲种配件的人数×原来平均每人每年可创造利润×(1+20%);生产乙种配件的年利润=生产乙种配件的人数×1.54m;总利润=调配后企业生产甲种配件的年利润+生产B种产品的年利润,把相关数值代入即可;
(2)关系式为:调配后企业生产甲种配件的年利润≥调配前企业年利润的五分之四,生产乙种配件的年利润>调配前企业年利润的一半,把相关数值代入求得x的取值范围,再根据x的实际意义确定其具体值,从而得出调配方案;
点评:本题考查一元一次不等式组的应用,一次函数的性质及方案选择问题,根据关键语句得到相应的关系式是解决问题的关键,难度一般.

 ,生产乙种配件的年利润大于调配前年利润的一半,应如何设计调配方案?哪种方案全年总利润最大?
,生产乙种配件的年利润大于调配前年利润的一半,应如何设计调配方案?哪种方案全年总利润最大?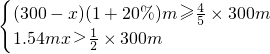 ,
, <x≤100,
<x≤100,
