
分析 (1)由点A、B在直线y=5x-6上,即可得出a2=5a-6、b2=5b-6,即a、b是方程x2-5x+6=0的两个根,通过解一元二次方程得出a、b的值,将其代入点A、B的坐标中即可得出结论;
(2)根据PA=PB、P、A、B三点共线,即可得出关于a、b的二元二次方程组,解方程求出a的值,将其代入点A的坐标中即可得出结论;
(3)由点P在直线y=-2x-2上,可设出点P的坐标,结合PA=PB、P、A、B三点共线,即可得出关于a、b、x的方程组,消去b即可得出关于a的一元二次方程,根据根的判别式△>0即可证出结论.
解答 解:(1)∵点A、B在直线y=5x-6上,
∴a2=5a-6,b2=5b-6,
即a、b是方程x2-5x+6=0的两个根,
∵a<b,
∴a=2,b=3,
∴点A的坐标为(2,4),点B的坐标为(3,9).
(2)∵PA=PB,P,A,B三点共线,
∴$\left\{\begin{array}{l}{a-(-2)=b-a}\\{{a}^{2}-2={b}^{2}-{a}^{2}}\end{array}\right.$,
解得:a=-1或a=-3,
∴点A的坐标为(-1,1)或(-3,9).
(3)证明:∵点P在直线y=-2x-2上,
∴设点P的坐标为(x,-2x-2).
∵PA=PB,P,A,B三点共线,
∴$\left\{\begin{array}{l}{a-x=b-a}\\{{a}^{2}-(2a-2)={b}^{2}-a}\end{array}\right.$,
消去b得:2a2-4ax+x2-2x-2=0.
∵△=(-4x)2-4×2×(x2-2x-2)=8(x+1)2+8≥8,
∴关于a的方程2a2-4ax+x2-2x-2=0恒有两个不相等的实数根,
∴对于直线y=-2x-2上任意给定的一点P,总能找到点A,使PA=AB成立.
点评 本题考查了一次函数图象上点的坐标特征、解一元二次方程组以及根的判别式,解题的关键是:(1)找出a、b是方程x2-5x+6=0的两个根;(2)找出关于a、b的二元二次方程组;(3)利用根的判别式恒大于0找出a值恒存在.本题属于中档题,难度不大,解决该题型题目时,根据一元二次方程的根的判别式恒大于0找出点存在是关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
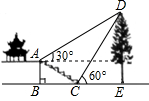 某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)
某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.
如图,AB为⊙O的直径,CO⊥AB于点O,D在⊙O上,连接BD、CD,延长CD与AB的延长线交于E,F在BE上,且FD=FE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
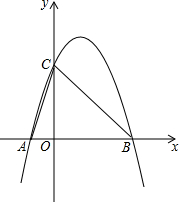 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax-3a的图象与x轴交于A、B两点(点B在点A的右侧),交y轴于点C,且S△ABC=6查看答案和解析>>
科目:初中数学 来源: 题型:填空题
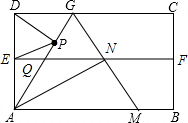 如图,四边形ABCD是矩形纸片,AD=2$\sqrt{3}$,对折矩形纸片ABCD,使AB与CD重合,折痕为EF;展平后再过点A折叠矩形纸片,使点D落在EF上的点N,折痕AG与EF相交于点Q;再次展平,连接AN,GN,延长GN交AB于点M,有如下结论:
如图,四边形ABCD是矩形纸片,AD=2$\sqrt{3}$,对折矩形纸片ABCD,使AB与CD重合,折痕为EF;展平后再过点A折叠矩形纸片,使点D落在EF上的点N,折痕AG与EF相交于点Q;再次展平,连接AN,GN,延长GN交AB于点M,有如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2或-2 | D. | -2或-$\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com