
分析 (1)利用二次根式的乘法法则运算;
(2)利用二次根式的除法法则运算;
(3)利用完全平方公式计算;
(4)先把各二次根式化简为最简二次根式,然后把括号内合并后进行二次根式的乘法运算;
(5)先利用积的乘方得到原式=[($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)]100•($\sqrt{3}$-2),然后利用平方差公式计算;
(6)利用零指数幂和负整数指数幂的意义计算.
解答 解:(1)原式=6$\sqrt{5×10}$=30$\sqrt{2}$;
(2)原式=$\sqrt{\frac{27}{3}}$-$\sqrt{\frac{12}{3}}$=3-2=1;
(3)原式=5-4+$\frac{4}{5}$=$\frac{9}{5}$;
(4)原式=2$\sqrt{3}$(15$\sqrt{3}$-2$\sqrt{3}$-3$\sqrt{3}$)=2$\sqrt{3}$×10$\sqrt{3}$=60;
(5)原式=[($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)]100•($\sqrt{3}$-2)
=(3-2)100•($\sqrt{3}$-2)
=$\sqrt{3}$-2;
(6)原式=1+4-(5-$\sqrt{3}$)-2$\sqrt{3}$
=5-5+$\sqrt{3}$-2$\sqrt{3}$
=-$\sqrt{3}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
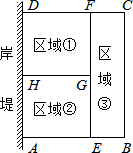 为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤长15m)为一边,用总长为80m的栅栏围在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为y m2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
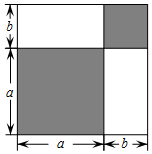 请认真观察图形,解答下列问题:
请认真观察图形,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在Rt△ABC中,∠C=90°,BC=4,AB=5,那么sinB的值是( )
在Rt△ABC中,∠C=90°,BC=4,AB=5,那么sinB的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com