
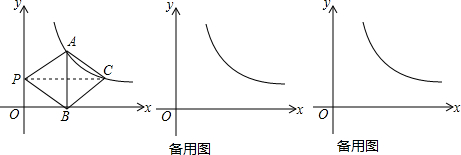
���� ��1������ƽ���ı��ε����ʱ�ʾ��A�����꣬�����÷���������ͼ���ϵ���������ʵó�k��m�Ĺ�ϵ��
��2���ɷ֡�APB=60��͡�PAC=60������������ۣ�Ȼ���������ε����ʼ����ɶ�����֪ʶ�Ϳɽ�����⣮
��� �⣺��1����AB��x�ᣬ��B������Ϊ��2��0������P��0��m����y���������ϵ�һ�����㣬��PA��PBΪ����ƽ���ı���APBC��
��AH=BH=m��PH=HC=2����A��2��2m����
��xy=k=4m��
��2������PC��AB�ڵ�H��
������APB=60�㣬��ͼ1��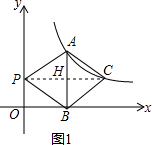
���ı���APBC�����Σ�
��PH=CH��BH=AH��AB��PC��PA=PB��
���PAB�ǵȱ������Σ�
��PB=AB=2BH��
��PH=$\sqrt{P{B}^{2}-B{H}^{2}}$=$\sqrt{3}$BH��
��PH=OB=2��
��$\sqrt{3}$BH=2��
��BH=$\frac{2\sqrt{3}}{3}$��
��m=OP=BH=$\frac{2\sqrt{3}}{3}$����A��������2��$\frac{4\sqrt{3}}{3}$����
�ߵ�A�ں���y=$\frac{k}{x}$ͼ���ϣ�
��k=2��$\frac{4\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$��
��ʱ��C������Ϊ��4��$\frac{2\sqrt{3}}{3}$����
��4��$\frac{2\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$=k��
���C��y=$\frac{k}{x}$��k��0����ͼ���ϣ�
������PAC=60�㣬��ͼ2��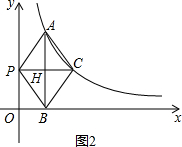
���ı���APBC�����Σ�
��PH=CH��BH=AH��AB��PC��PA=PB��
���PCB�ǵȱ������Σ�
��PB=PC=2PH=4��
��OP=2$\sqrt{3}$����C����������4��2$\sqrt{3}$����
�ɵã�k=8$\sqrt{3}$��m=2$\sqrt{3}$��
��C������Ϊ��4��2$\sqrt{3}$������y=$\frac{k}{x}$��k��0����ͼ���ϣ�
���� ���⿼���˷����������ۺϡ�ƽ���ı��ε����ʡ����ε����ʡ��ȱ������ε��ж������ʡ����ɶ�����֪ʶ�����÷������۵���ѧ˼������ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30cm2 | B�� | 30��cm2 | C�� | 15��cm2 | D�� | 15cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com