
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
| 49 |
| 2 |
| 49 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:同步轻松练习 八年级 数学 上 题型:022
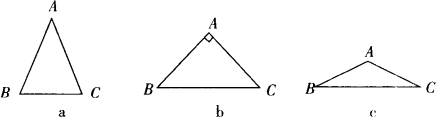
如图,现有顶角度数互不相同的等腰三角形(AB=AC)纸片(图a、图b、图c)3块,其中有的能从一个底角的顶点出发,将原纸片一次剪开成两块等腰三角形纸片.(1)能剪成两块等腰三角形的纸片是________,并用尺规在选中的图上作出你的剪痕(用虚线表示),虚线另一端标上字母T;(2)将所选图中的相等线段填写在下列对应的横线上(未选中的不要填写,线段相等用等式表示,AB=AC除外):a图________,b图________,c图________;(3)选中的等腰三角形的顶角度数为________(若选中两种及以上只计算一种).
查看答案和解析>>
科目:初中数学 来源:2013届北京市八年级上学期期中数学试卷(解析版) 题型:解答题
如图1,给你一张三角形纸片,其中AB=AC, ∠A=36°,将此纸片按图2中的线剪开,可以将原三角形分成三个等腰三角形,那么
(1)仿照图2,再设计两种不同的分割方法,将原三角形纸片分为3个三角形,使得每个三角形都为等腰三角形.
(2)仿照图2,再设计一种不同的分割方法,将原三角形纸片分为4个三角形,使得每个三角形都为等腰三角形.
(要求:在图中标出分得的每个等腰三角形的三个内角的度数)


|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com