
分析 由a>b>0,且a+b+c=0,可以判定c<0,与y轴交于负半轴,抛物线y=ax2+bx+c开口向上,对称轴x=-$\frac{b}{2a}$<0,$\frac{4ac-{b}^{2}}{4a}$<0,顶点坐标在第三象限,由此画出函数的图象即可.
解答 解:∵a>b>0,且a+b+c=0,
∴c<0,与y轴交于负半轴,抛物线y=ax2+bx+c开口向上,对称轴x=-$\frac{b}{2a}$<0,$\frac{4ac-{b}^{2}}{4a}$<0,顶点坐标在第三象限.
图象如下: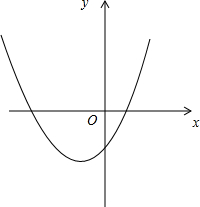
点评 本题考查了二次函数的图象,根据条件判定抛物线的开口方向、对称轴、顶点坐标与、y轴交点坐标是解决问题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
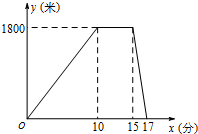 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表 示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是( )
某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表 示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是( )| A. | 小明在公园休息了5分钟 | B. | 小明乘出租车用了17分 | ||
| C. | 小明跑步的速度为180米/分 | D. | 出租车的平均速度是900米/分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,此蜡烛经过( )小时燃烧完毕.
如图是某种蜡烛在燃烧过程中高度与时间之间关系的图象,此蜡烛经过( )小时燃烧完毕.| A. | 2 | B. | $\frac{15}{4}$ | C. | $\frac{15}{8}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com