
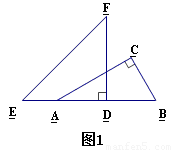
将一幅三角板Rt△ABC和Rt△DEF按如图1摆放,点E, A, D, B在一条直线上,且D是AB的中点,将Rt△DEF绕点D顺时针方向旋转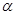 (0°<
(0°<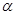 <90°)角,在旋转过程中,直线DE与AC相交于点M,直线DF与BC相交于点N,分别过点M, N作直线AB的垂线,垂足分别为G, H.
<90°)角,在旋转过程中,直线DE与AC相交于点M,直线DF与BC相交于点N,分别过点M, N作直线AB的垂线,垂足分别为G, H.
(1)当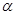 =30°时(如图2),求证:AG=DH;
=30°时(如图2),求证:AG=DH;
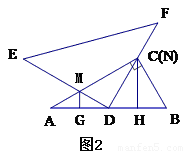
(2)当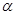 =60°时(如图3),(1)中的结论是否仍成立?请写出你的结论,并说明理由.
=60°时(如图3),(1)中的结论是否仍成立?请写出你的结论,并说明理由.
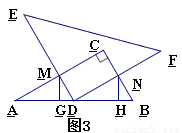
见解析.
【解析】
试题分析:(1)由α=30°知∠ADM=30°,∠A=30°,所以∠ADM=∠A.AM=DM.又由MG⊥AD于G,可得:AG= 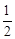 AD.又有∠CDB=180°-∠EDF-∠ADM=60°,∠B=60°,证得△CDB是等边三角形.又CH⊥DB于H,DH=
AD.又有∠CDB=180°-∠EDF-∠ADM=60°,∠B=60°,证得△CDB是等边三角形.又CH⊥DB于H,DH= 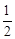 DB.根据直角三角形中30°所对直角边是斜边的一半得:BC=
DB.根据直角三角形中30°所对直角边是斜边的一半得:BC= 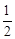 AB.由BC=BD,所以有AD=DB.从而证得AG=DH.
AB.由BC=BD,所以有AD=DB.从而证得AG=DH.
(2)在△AMD与△DNB中,∠A=∠NDB=30°,AD=DB,∠MDA=∠B=60°,可得△AMD≌△DNB,所以AM=DN.在△AMG与△DNH中,∠A=∠NDB,∠MGA=∠NHD=90°,又可证得△AMG≌△DNH.
∴AG=DH.
试题解析:(1)∵α=30°,∴∠ADM=30°,
∵∠A=30°,∴∠ADM=∠A.
∴AM=DM.
又∵MG⊥AD于G,
∴AG= 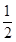 AD.
AD.
∵∠CDB=180°-∠EDF-∠ADM=60°,∠B=60°,
∴△CDB是等边三角形.
又∵CH⊥DB于H,
∴DH= 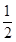 DB.
DB.
∵在△ABC中,∠ACB=90°,∠A=30°,
∴BC= 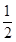 AB.
AB.
∵BC=BD,∴AD=DB.
∴AG=DH.
(2)结论成立.理由如下:
在△AMD与△DNB中,∠A=∠NDB=30°,AD=DB,∠MDA=∠B=60°,
∴△AMD≌△DNB,
∴AM=DN.
又∵在△AMG与△DNH中,∠A=∠NDB,∠MGA=∠NHD=90°,
∴△AMG≌△DNH.
∴AG=DH .
考点:1.等边三角形的判定.2.直角三角形30°所对的直角边等于斜边的一半.3. 全等三角形判定和性质.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:
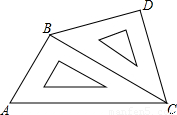
 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)| 22+22 |
| 2 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
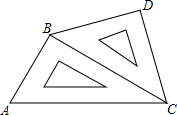 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)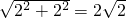
查看答案和解析>>
科目:初中数学 来源:2009-2010学年天津市河西区九年级(上)期末数学试卷(解析版) 题型:解答题
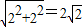
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com