
分析 (1)直接利用等腰三角形的性质结合锐角三角函数关系求出答案;
(2)直接利用等腰三角形的性质结合锐角三角函数关系求出答案.
解答 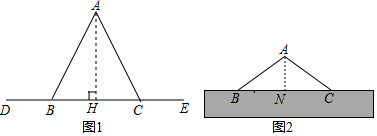 解:(1)如图1,过点A作AH⊥BC于点H,
解:(1)如图1,过点A作AH⊥BC于点H,
∵AB=AC,绳子与水平线夹角为72°,绳子的总长为30cm,
∴AB=AC=15cm,∠ACB=∠ABC=72°,
∴cos72°=$\frac{BH}{AB}$=$\frac{BH}{15}$≈0.31,
解得:BH=4.65,
故BC=2BH=9.3(cm),
答:袋子两支点BC的距离为9.3cm;
(2)如图2,过点A作AN⊥BC于点N,
∵BC=9.3cm,
∴BN=CN=4.65cm,
∵绳子与水平线的夹角为30°,
∴∠ABC=∠ACB=30°,
∴cos30°=$\frac{BN}{AB}$=$\frac{4.65}{AB}$=$\frac{\sqrt{3}}{2}$,
解得:AB≈5.4(cm),
∴绳子减少的长度为:15-5.4=9.6(cm).
点评 此题主要考查了解直角三角形的应用,正确利用等腰三角形的性质是解题关键.


科目:初中数学 来源: 题型:填空题
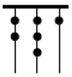 古时候,猎人通过结绳的方法来统计猎物的个数,如图,一位猎人在排列的绳子上从右到左依次打结,满八进一,用来记录一段时间内猎物的数量,由图可知,猎物的数量是153.
古时候,猎人通过结绳的方法来统计猎物的个数,如图,一位猎人在排列的绳子上从右到左依次打结,满八进一,用来记录一段时间内猎物的数量,由图可知,猎物的数量是153.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
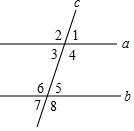 如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )
如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6②∠1=∠7③∠1+∠4=180°④∠3=∠8,其中能推断a∥b的条件的序号是( )| A. | ①② | B. | ①③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com