
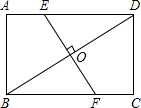
 如图,O是矩形ABCD的对角线BD的中点,过点O的直线EF垂直BD,交AD于点E,交BC于点F,AE=5cm,DE=13cm,则矩形ABCD的周长为________cm.
如图,O是矩形ABCD的对角线BD的中点,过点O的直线EF垂直BD,交AD于点E,交BC于点F,AE=5cm,DE=13cm,则矩形ABCD的周长为________cm.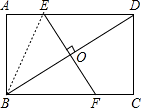


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
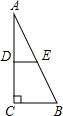 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初二数学 华东师大(新课标2001-3年初审) 华东师大(新课标2001-3年初审) 题型:044
如图,BO是Rt△ABC斜边上的中线,延长BO至点D,使DO=BO,连结AD,CD,则四边形ABCD是矩形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东揭阳揭西张武帮中学九年级上质检考试数学试卷B(解析版) 题型:选择题
如图,AC.BD是矩形ABCD的对角线,过点D作DF∥AC交BC的延长线于F,则图中与△ABC全等的三角形共有( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com