
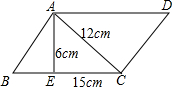
 如图所示,AC=12cm,AE=6cm,BC=15cm,AE⊥BC于点E,求平行四边形ABCD的周长.
如图所示,AC=12cm,AE=6cm,BC=15cm,AE⊥BC于点E,求平行四边形ABCD的周长. 分析 首先在Rt△AEC中求出AE,再在Rt△ABE中求出AB即可解决问题.
解答 解:在Rt △AEC中,∵∠AEC=90°,AC=12,AE=6,
△AEC中,∵∠AEC=90°,AC=12,AE=6,
∴EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=6$\sqrt{3}$,
∵BC=15,
∴BE=15-6$\sqrt{3}$,
在Rt△ABE中,AB=$\sqrt{B{E}^{2}+A{E}^{2}}$=$\sqrt{369-180\sqrt{3}}$,
∴平行四边形ABCD的周长=2(AB+BC)=2($\sqrt{369-180\sqrt{3}}$+15)=(2$\sqrt{369-180\sqrt{3}}$+30)cm.
点评 本题考查平行四边形的性质、勾股定理等知识,解题的关键是灵活应用所学知识解决问题,属于基础题,参考常考题型.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
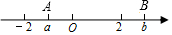 如图,A、B两点在数轴上表示的数为a、b,下列式子成立的是( )
如图,A、B两点在数轴上表示的数为a、b,下列式子成立的是( )| A. | a+b<0 | B. | ab>0 | C. | (b-2)(a+2)>0 | D. | (b-2)(a-2)>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.334×107人 | B. | 3.34×106人 | C. | 33.4×105人 | D. | 3.34×102人 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
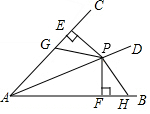 如图,已知:P是∠AOB平分线上一点,PE⊥OA,PF⊥OB,垂足分别是E,F,G,H分别是OA,OB上两点,且PG=PH,求证:EG=FH.
如图,已知:P是∠AOB平分线上一点,PE⊥OA,PF⊥OB,垂足分别是E,F,G,H分别是OA,OB上两点,且PG=PH,求证:EG=FH.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{17}{4}$ | C. | $\frac{5}{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com