
| 4 |
| 5 |

| 4 |
| 5 |
| EF |
| AC |
| BE |
| BC |
| 5 |
| 8 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| EF |
| AC |
| BE |
| BC |
| 5 |
| 8 |
| 5 |
| 8 |
| 4 |
| 5 |
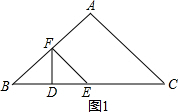
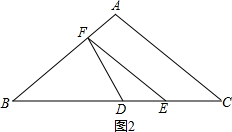 ∴FD=
∴FD=| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 27 |
| 8 |
| 5 |
| 8 |
| 4x |
| 5 |
| 75 |
| 7 |
| 1 |
| 2 |
| 75 |
| 7 |
| 4 |
| 5 |
| 75 |
| 7 |
| 3 |
| 5 |
| 1350 |
| 49 |
| 13 |
| 4 |


科目:初中数学 来源: 题型:
| 第一档电价 | 第二档电价 | 第三档电价 |
| 月用电50千瓦时及以下部分,每千瓦时价格0.538元 | 月用电51--200千瓦时部分,每千瓦时比第一档提价0.03元 | 月用电201千瓦时及以上部分,每千瓦时比第一档提价0.10元 |
| 第一档电价 | 第二档电价 | 第三档电价 |
| 年用电2760千瓦时及以下部分,每千瓦时价格0.538元 | 年用电2761--4800千瓦时部分,每千瓦时比第一档提价0.05元 | 年用电4801千瓦时及以上部分,每千瓦时比第一档提价0.30元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据:
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据:| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
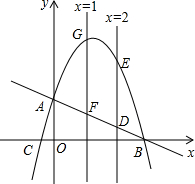 如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+
如图,抛物线与x轴相交于B、C两点,与y轴相交于点A,P(a,-a2+| 7 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).查看答案和解析>>
科目:初中数学 来源: 题型:
 【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断)
【倾听理解】(这是习题讲评课上师生围绕一道习题的对话片断) |
| BC |
 |
| AC |
 |
| BC |
 |
| AC |
查看答案和解析>>
科目:初中数学 来源: 题型:
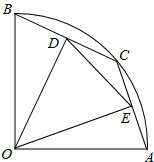
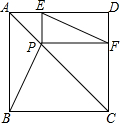 如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足,
如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com