
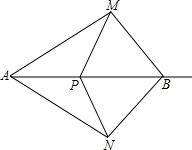
 如图,AM=AN,BM=BN.
如图,AM=AN,BM=BN.
|
|


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:044
如图①,直线AM⊥AN, ⊙O分别与AM、AN相切于B、C两点,连结OC、BC,则有∠ACB=∠OCB;(请思考:为什么?)如果测得AB=a,则可知⊙O的半径r=a.(请思考:为什么?)
(1)将图①中直线AN向右平移,与⊙O相交于C1、C2两点,⊙O与AM的切点仍记为B,如图②.请你写出与平移前相应的结论,并将图②补充完整;判断此结论是否成立,且说明理由.


(2)
在图②中,若只测得AB=a,能否求出⊙O的半径r?若能求出,请你用a表示r;若不能求出,请补充一个条件(补充条件时不能添加辅助线,若补充线段请用b表示,若补充角请用α表示),并用a和补充的条件表示r.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
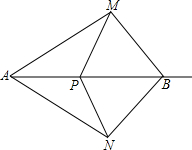 如图,AM=AN,BM=BN.
如图,AM=AN,BM=BN.查看答案和解析>>
科目:初中数学 来源:第3章《圆》中考题集(35):3.5 直线和圆的位置关系(解析版) 题型:填空题
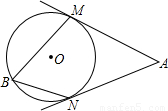
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com