
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y2>y1 | D. | y1>y3>y2 |
分析 先确定对称轴和二次项系数,利用增减性可知:当x>1时,y随x的增大而增大,并由对称性得:x=-1与x=3时对应的y相等,因此把要比较的三个点都放在对称轴的同侧,则由3>2>$\sqrt{2}$>1,得y1>y3>y2.
解答 解:对称轴是:直线x=1,
∵3>0,
∴当x>1时,y随x的增大而增大,
当x<1时,y随x的增大而减小,
由对称性得:x=-1与x=3时对应的y相等,
∵3>2>$\sqrt{2}$>1,
∴y1>y3>y2,
故选D.
点评 本题考查了二次函数图象上点的坐标特征,本题可以代入计算比较大小,也可以利用增减性来比较;因此要熟练掌握二次函数的增减性,利用增减性比较x或y的大小关系,熟记当a>0时,对称轴的右侧,y随x的增大而增大,对称轴的左侧,y随x的增大而减小,当a<0时,对称轴的右侧,y随x的增大而减小,对称轴的左侧,y随x的增大而增大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“玩具车”的次数m | 67 | 111 | 143 | 347 | 567 | 702 |
| 落在“玩具车”的频率 | 0.67 | 0.74 | 0.715 | 0.694 | 0.705 | a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
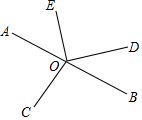 如图,点O在直线AB上,OC是∠AOB的平分线,在直线AB的另一侧以点O为顶点作∠DOE=90°
如图,点O在直线AB上,OC是∠AOB的平分线,在直线AB的另一侧以点O为顶点作∠DOE=90°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com