【答案】
分析:由于ab>0,那么a、b同号,当a>0,b>0时,直线经过第一、二、三象限,双曲线经过第一、二象限,当a<0,b<0时,直线经过第二、三、四象限,双曲线经过第二、四象限,利用这些结论即可求解.
解答:解:∵ab>0,
∴a、b同号,
当a>0,b>0时,直线经过第一、二、三象限,双曲线经过第一、三象限,
当a<0,b<0时,直线经过第二、三、四象限,双曲线经过第二、四象限,
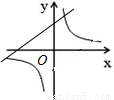
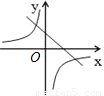
A、图中直线经过直线经过第一、四、三象限,双曲线经过第一、三象限,故选项错误;
B、图中直线经过原点,故选项错误;
C、图中直线经过第一、二、三象限,双曲线经过第一、三象限,故选项正确;
D、图中直线经过第二、一、四象限,双曲线经过第二、四象限,故选项错误.
故选C.
点评:此题考查一次函数,反比例函数中系数及常数项与图象位置之间关系.直线y=kx+b、双曲线y=
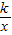
当k>0时经过第一、三象限,当k<0时经过第二、四象限.

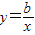 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )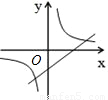
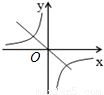
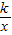 当k>0时经过第一、三象限,当k<0时经过第二、四象限.
当k>0时经过第一、三象限,当k<0时经过第二、四象限. 
