
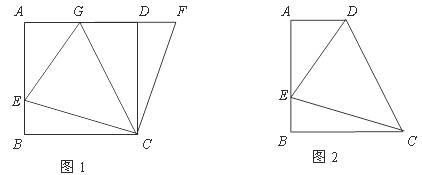
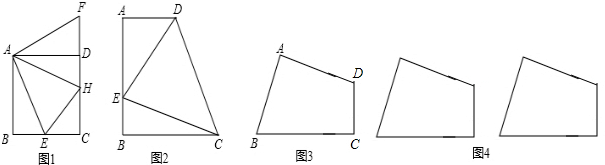
如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
⑴求证:CE=CF;
⑵在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
⑶运用⑴⑵解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
| |
⑴证明:在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF.
∴CE=CF.
⑵解:GE=BE+GD成立.
∵△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠ECD+∠ECB=∠ECD+∠FCD
即∠ECF=∠BCD=90°,
又∠GCE=45°,∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCF=∠GCE,GC=GC,
∴△ECG≌△FCG.
∴EG=GF.
∴GE=DF+GD=BE+GD.
⑶解:过C作CG⊥AD,交AD延长线于G.
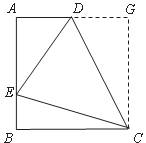
在直角梯形ABCD中,
∵AD∥BC,∠A=∠B=90°,
又∠CGA=90°,AB=BC,
∴四边形ABCD 为正方形.
∴AG=BC=12.
已知∠DCE=45°,根据⑴⑵可知,ED=BE+DG.
设DE=x,则DG=x-4,
∴AD=16-x.
在Rt△AED中,
∵![]() ,即
,即![]() .
.
解得:x=10.
∴DE=10.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
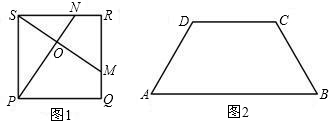 构造一个与上述命题类似的正确命题并加以证明.
构造一个与上述命题类似的正确命题并加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:
 26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.
26、如图1,在正方形ABCD中,若点E是△DBC内的一点,且DE=DC,BE=CE.查看答案和解析>>
科目:初中数学 来源: 题型:
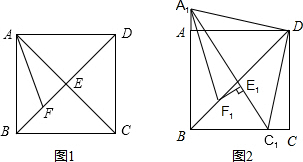 如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.
如图1,在正方形ABCD中,对角线AC与BD相交于点E,AF平分∠BAC,交BD于点F.| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com