
 与以下那个数相乘,结果是有理数?
与以下那个数相乘,结果是有理数?

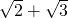


 相乘结果是有理数的数.
相乘结果是有理数的数. 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:三点一测丛书八年级数学上 题型:044
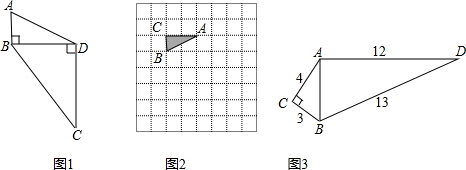
教科书(华东师范大学版)P45页有这样一篇阅读材料:
黄金矩形看一看雅典帕德嫩神庙的造型,甚至现在这还是世界最美丽的建筑之一,这神庙建筑于古希腊数学繁荣的年代,并且它的美丽就是建立在严格的数学法则上的.如果我们在帕德嫩神庙周围描一个矩形,那么发现,它的长大约是宽的1.6倍,这种矩形称为黄金矩形.
问题:你会用圆规与三角板画一个以所给正方形的边长为宽的黄金矩形吗?试试看,在图上画出图形来.

查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第19~26期 总第175~182期 华师大版 题型:044
从前有个国王,他有三个儿子.大王子只喜欢读书,二王子只知道习武,小王子的兴趣十分广泛,爱读书,爱习武,还爱玩.
有一天,国王对王子们说:“你们的祖父母去世早,你们可能都记不得他们的年龄了,谁能告诉我,你们的祖父母都活了多大岁数?”
二王子问:“可以问您几个问题吗?”
国王回答:“只能问一个.”
“啊,问一个问题就猜到祖父母的年龄,太困难了,这恐怕连神仙也难办到!”大王子自言自语地说.
国王又问小王子说:“你行吗?”小王子点了点头.大王子和二王子都很惊讶.
小王子说:“请您把祖父的年龄放在前面、祖母的年龄放在后面,组成一个四位数,然后将这个四位数平方,接着减去祖母年龄的平方,然后除以祖父年龄的100倍,最后减去祖母的年龄,把所得的数告诉我.”
国王不知道小王子想干什么,心算了一阵说:“得3129”.
小王子马上答道:“祖父活到31岁,祖母活到29岁.”国王高兴地站起来说:“对极啦,就是这两个年龄!”“为什么让父王算一道题,就能把祖父母的年龄算出来呢?”“只许问一个问题,要猜出两人的年龄,还不能直接去问,你是怎样算的呢?”两位哥哥不停地问着小王子.
小王子的妙算是让父王算出一个四位数,使得千位和百位上的数字与祖父的年龄有关;十位和个位上的数字与祖母的年龄有关.
小王子的算法是:祖父的年龄放在前面、祖母的年龄放在后面组成的四位数是3129,将这个四位数平方,得9790641;减去祖母年龄的平方,得9789800;除以祖父年龄的100倍,得3158;最后减去祖母的年龄,得(31292-292)÷(31×100)-29=3129.
大王子问:“为什么这样一定可以得到3129呢?”
小王子解释,可以利用整式的乘除的知识,把上面的算式以另一种方式做一下变形:
[(31×100+29)2-292]÷3100-29=(312×1002+2×31×100×29+292-292)÷3100-29=(312×1002+2×31×100×29)÷3100-29=31×100+2×29-29=3129.
原来小王子像魔术师变魔术一样,在计算中加了一点“伪装”,这就是“将四位数平方,减去祖母年龄的平方,除以祖父年龄的100倍,减去祖母的年龄”.其实这些步骤与计算祖父、祖母的年龄毫无关系,目的是使这种计算更隐蔽、更神秘(其实,我们只需根据由祖父、祖母年龄组成的四位数就可以知道祖父、祖母的年龄).
同学们,你能通过整式的有关知识对小王子的算法作出解释吗?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
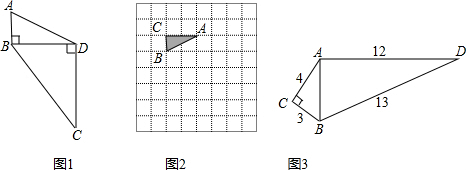
查看答案和解析>>
科目:初中数学 来源:2012年贵州省贵阳市中考数学模拟试卷(四)(解析版) 题型:解答题
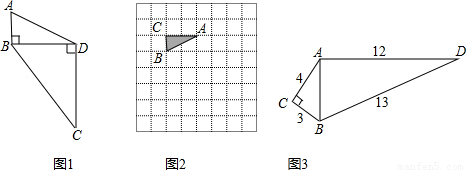
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com