
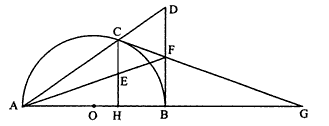
| 解:(1)∵CH⊥AB,DB⊥AB, ∴△AEH∽AFB,△ACE∽△ADF, ∴ 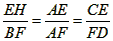 , ,∵HE=EC, ∴BF=FD; (2)连接CB、OC, ∵AB是直径, ∴∠ACB=90°, ∵F是BD中点, ∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO, ∴∠OCF=90°, ∴CG是⊙O的切线; (3)由FC=FB=FE得:∠FCE=∠FEC, 可证得:FA=FG,且AB=BG, 由切割线定理得:(2+FG)2=BG×AG=2BG2 ①, 在Rt△BGF中, 由勾股定理得:BG2=FG2-BF2 ② 由①、②得:FG2-4FG-12=0, 解之得:FG1=6,FG2=-2(舍去) ∴AB=BG= 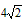 , ,∴⊙O半径为2 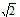 。 。 |
 |


科目:初中数学 来源: 题型:
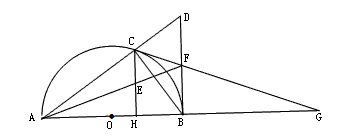
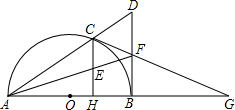 点D,E为CH的中点,连接AE并延长交BD于F,直线CF交直线AB于点G.
点D,E为CH的中点,连接AE并延长交BD于F,直线CF交直线AB于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
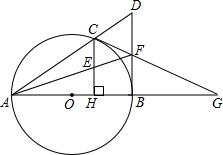 (2012•德阳)如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(2012•德阳)如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.查看答案和解析>>
科目:初中数学 来源: 题型:
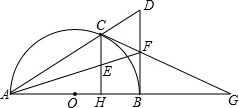 如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com